单词

mathematical induction

释义

mathematical induction

The method of proof ‘by mathematical induction' is based on the following principle:

Principle of mathematical induction

Let there be associated, with each positive integer n, a proposition P(n), which is either true or false. If

(i) P(1) is true,

(ii) for all k, P(k) implies P(k + 1),

then P(n) is true for all positive integers n.

The following are typical of results that can be proved by induction:

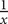(a) For all positive integers n, $inline$ .

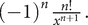
(b) For all positive integers n, the nth derivative of $inline$ is $inline$

In each case, it is clear what the proposition P(n) should be and that (i), the base case, can be verified. The method by which the so‐called inductive step (ii), where the inductive hypothesis P(k) is assumed, is proved depends upon the particular result to be established.

There is a so-called ‘strong form' of the principle of induction which is equivalent. It states:

(i') P(1) is true,

(ii') for all k, the truth of P(1), P(2), …, P(k–1), P(k) implies P(k + 1),

then P(n) is true for all positive integers n.

This is a useful alternative when the inductive step proving P(k + 1) relies on the truth of some previous proposition P(i) which is not necessarily P(k).

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。