tensor

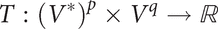
where V denotes the dual space. The order of the tensor is p + q, and the tensor may also be considered as a (p + q)-dimensional array once bases are chosen. If p = 0, the tensor is called covariant, and if q = 0, the tensor is called contravariant. If V = Rn, then the tensor is called Cartesian.

Let e1,…, en be a basis of V and f1,…,fn be the dual basis. When p = 0, q = 1, T is a functional, and when p = 1, q = 0, T is a vector v = (Tf1,…,Tfn). When p = q = 1, then T represents a linear map T:V → V as follows: T is represented by the matrix (aij), where

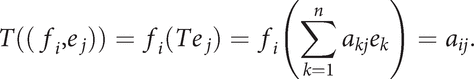
More properly, considered as a tensor, these entries should be written 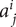to denote that one of these indices is covariant, one contravariant. See also Einstein's notation.

Tensors appear widely throughout mathematics and physics; grad is a (0,1) tensor, an inner product is a (0,2) tensor, as is the first fundamental form, the vector product is a (1,2) tensor, stress and strain are tensors, and differential forms are tensors. The first fundamental form on a surface instead might be considered as assigning an inner product, a tensor, to each tangent space; this is an example of a tensor field, important in physics and general relativity particularly.

• completely balanced block design
• completely normal space
• completely regular space
• complete matching
• complete metric space
• completeness axiom of the real numbers
• complete orthonormal basis
• complete quadrangle
• complete set of residues
• complete solution
• completing the square
• completion
• complex analysis
• complex analytic
• complex conjugate
• complex exponential
• complex function
• complexity
• complex logarithm
• complex number
• complex plane
• complex potential
• complex system
• component
• component