change of basis for V and
for V and 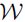 for W, then the matrix of the linear map T sends the coordinate vector of v ∈ V to the coordinate vector of Tv in W. Denote this matrix as
for W, then the matrix of the linear map T sends the coordinate vector of v ∈ V to the coordinate vector of Tv in W. Denote this matrix as 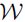 T
T . If
. If  ' and
' and 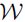 ' are two other bases, then
' are two other bases, then 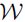 'T
'T ' = (
' = (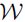 ' I
' I 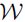 )(
)(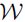 T
T  )(
)( I
I  '), where I denotes the identity map (on V or W). The matrices
'), where I denotes the identity map (on V or W). The matrices 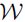 ' I
' I 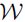 and
and  I
I  ' are referred to as change of basis matrices. Respectively, they change the coordinates of a vector with respect to
' are referred to as change of basis matrices. Respectively, they change the coordinates of a vector with respect to 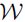 (or
(or  ') to the coordinates of the same vector with respect to
') to the coordinates of the same vector with respect to 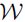 ' (or
' (or  ).
).
- Hilbert's programme
- Hilbert's tenth problem
- Hindu-Arabic number system
- histogram
- history of mathematics
- holomorphic
- holonomic
- Hom
- homeomorphism
- homogeneous
- homogeneous
- homogeneous coordinates
- homogeneous first‐order differential equation
- homogeneous linear differential equation
- homogeneous polynomial
- homogeneous set of linear equations
- homomorphism
- homoscedastic
- homotopy
- homotopy equivalence
- Hooke's law
- Horner's rule
- Householder transformation
- Hoyles, Dame Celia
- Huffman coding