circle theorems
(i) Let A and B be two points on a circle with centre O. If P is any point on the circumference of the circle and on the same side of the chord AB as O, then ∠AOB = 2∠APB. Hence the ‘angle at the circumference' ∠APB is independent of the position of P.
(ii) If Q is a point on the circumference and lies on the other side of AB from P, then ∠AQB = 180°-∠APB. Hence opposite angles of a cyclic quadrilateral (see cyclic polygon) add up to 180°.
(iii) When AB is a diameter, the angle at the circumference is the ‘angle in a semicircle' and is a right angle.
(iv) If T is any point on the tangent at A, then ∠APB = ∠BAT.
(v) Suppose now that a circle and a point P are given. Let any line through P meet the circle at points A and B. Then PA. PB is constant; that is, the same for all such lines. If P lies outside the circle and a line through P touches the circle at the point T, then PA.PB = PT2.
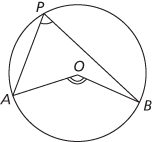
(i) ∠AOB = 2∠APB
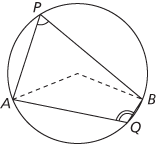
(ii) ∠AQB = 180°−∠APB
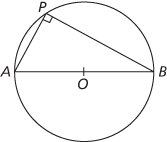
(iii) A diameter subtends a right angle
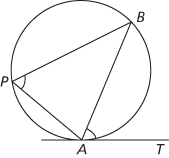
(iv) ∠APB = ∠BAT

(v) PA.PB = PT2 is constant
- hcf
- heat
- heat equation
- Heaviside function
- hectare
- hecto‐
- height
- Heine-Borel theorem
- Heisenberg's uncertainty principle
- Heisenberg, Werner Karl
- helicoid
- helix
- hemisphere
- hemi‐
- hendecagon
- heptagon
- hepta‐
- hereditary property
- Hermite, Charles
- Hermite polynomials
- Hermitian
- Hermitian conjugate
- Hero (Heron) of Alexandria
- Hero's formula
- Hero's method