“higher‐order partial derivative”的概念、定义、习题解题方法及翻译-数学辞典

单词

higher‐order partial derivative

释义

higher‐order partial derivative

Given a function f of n variables x1, x2,…, xn, the partial derivative ∂f/∂xi, where 1 ≤ i ≤ n, may also be reckoned to be a function of x1, x2,…, xn. So the partial derivatives of ∂f/∂xi can be considered. Thus

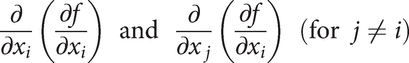
can be formed, and these are denoted, respectively, by

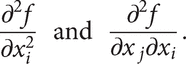
These are the second‐order partial derivatives. When j ≠ i,

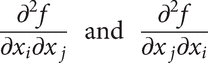
are different by definition, but the two are equal for most ‘straightforward' functions f—it is sufficient that either mixed derivative be continuous. Similarly, third‐order partial derivatives such as

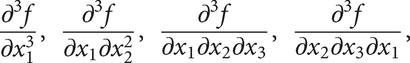
can be defined, and so on. Then the nth‐order partial derivatives, where n≥2, are called the higher‐order partial derivatives.

When f is a function of two variables x and y, and the partial derivatives are denoted by fx and fy, then fxx, fxy, fyx, fyy are used to denote

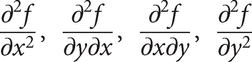
respectively, noting particularly that fxy means (fx)y and fyx means (fy)x. Alternatively, these partial derivatives fx and fy of f(x,y) are denoted by f1 and f2, with similar notations for the higher-order partial derivatives.

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。