Morse Theory

A Morse function on a smooth surface is a smooth real function with only non-degenerate stationary points (see Hessian), and so these are local maxima, local minima, or saddle points. For any smooth function f on a closed, smooth manifold X, it is the case that

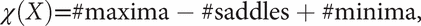
where χ(X) denotes the Euler characteristic of X and #maxima denotes the number of maxima, etc. In the figure is a cross-section of a torus and f(x,y,z) = z is a Morse function on the torus. f has a maximum at D, a minimum at A, and saddle points at B and C. This correctly gives χ = 1 − 2 + 1 = 0.

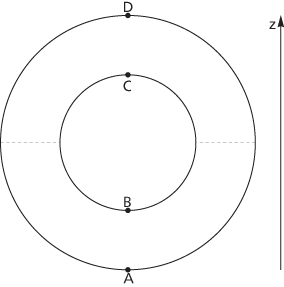
The height function on the torus

Morse theory includes results for the subsets of the surface of the form f ≤ k. In the figure, such a subset is that part of the torus below the dotted lines. For any z-coordinate k between B and C Morse theory states the subsets are homotopy equivalent. Further, the theory states how the homotopy type of the subset f ≤ k changes as k takes a stationary value.

• rough surface
• round
• round angle
• rounding
• round-off error
• route inspection problem
• row
• row equivalence
• row operation
• row rank
• row space
• row vector
• Royal Institution
• RRE form
• RSA
• ruled surface
• ruler and compass construction
• run
• run
• Runge–Kutta methods
• Russell, Bertrand Arthur William
• Russell's paradox
• Rutherford, Lord
• rv
• saddle-point