dual space (algebraic)
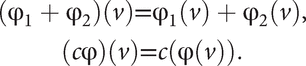
If V is finite-dimensional, then V has the same dimension (see dual basis).
- inertial frame of reference
- inertial mass
- inertia matrix
- inextensible string
- inf
- infeasible
- inference
- infimum
- infinite
- infinite product
- infinite sequence
- infinite series
- infinite set
- infinitesimal
- infinity
- inflection
- information
- information theory
- inhomogeneous
- initial conditions
- initialize
- initial line
- initial value
- initial value problem
- injection