Attracting fixed point |g'(α)|<1

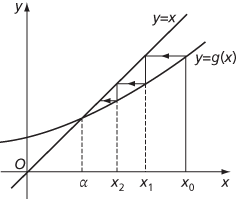
A root of x = g(x) occurs where the graph y = g(x) meets the line y = x. It can be shown that, if |g′(α)|<1, then the sequence converges for suitably close initial values x0, and α is called attracting. If |g′(α)|>1, then the sequence diverges from α for nearby initial values x0. This is illustrated in the figures; such diagrams are called ‘cobweb plots', and the process is called ‘cobwebbing'. The equation x3−x−1=0 has a root α between 1 and 2, so we take x0=1.5. The equation can be written in the form x = g(x) in several ways, such as (i) x = x3−1 or (ii) x = (x + 1)1/3. In case (i), g′(x)=3x2, g′(α) > 3 > 1 and so α is repelling for this iteration; in case (ii), and g′(α)<2−2/3/3<1 and so α is attractive.

More generally a fixed point α ∈ X of a function f:X→X is attracting if the fixed-point iteration converges to α for initial values in a neighbourhood of α and is repelling if there is a neighbourhood of α such that the fixed-point iteration eventually moves out of the neighbourhood for all initial values other than α.