单词

integration

释义

integration

The process of finding an antiderivative of a given function f. ‘Integrate f' means ‘find an antiderivative of f'. Such an antiderivative may be called an indefinite integral of f and be denoted by

Such antiderivatives are only defined up to addition of an arbitrary constant.

The term ‘integration' is also used for any method of evaluating a definite integral. The definite integral

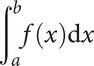
can be evaluated if an antiderivative ϕ of f can be found, because then its value is ϕ(b)−ϕ(a). (This is provided that a and b both belong to an interval in which f is continuous.) However, for many functions f, it can be shown there is no antiderivative expressible in terms of elementary functions, and other methods of evaluation have to be employed such as numerical integration.

What ways are there, then, of finding an antiderivative? If the given function can be recognized as the derivative of a familiar function, an antiderivative is immediately known. For some standard integrals, see appendix 8; more extensive tables of integrals are available. Certain techniques of integration may also be tried, among which are the following:

Change of variable/Substitution

If it is possible to find a suitable function g such that the integrand can be written as f(g(x)) g′(x), it may be possible to find an indefinite integral using the change of variable u = g(x); this is because

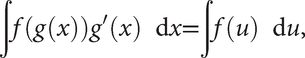
a rule derived from the chain rule for differentiation. For example, in the integral

let u = g(x) = x2 + 1. Then g′(x) = 2x (this can be written ‘du = 2x dx'), and, using the rule above with f(u) = u8, the integral equals

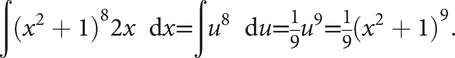
Commonly, it may seem more natural to treat x as a function of u and ‘substitute' x = g(u) according to

Note in the following example of a definite integral that it is necessary to change from x-limits to u-limits.

Let x = g(u) = tanu. Then g′(u) = sec2u (this can be written ‘dx = sec2u du'), and recalling 1 + tan2u = sec2u, the integral becomes

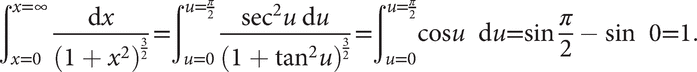
Integration by parts

The rule for integration by parts,

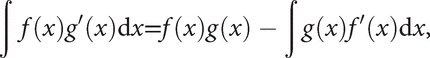
is derived from the rule for differentiating a product f(x)g(x), and is useful when the integral on the right‐hand side is easier to find than the integral on the left. For example, in the integral

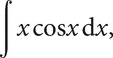
let f(x) = x and g′(x) = cos x. Then g(x) can be taken as sin x and f′(x) = 1, so the method gives

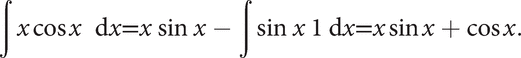
See also integrable, Lebesgue integral, partial fractions, reduction formula, separable first‐order differential equations.

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。