p-adic numbers
A p-adic integer is a sequence of the form (x0, x1, x2, …) such that xn ≡ xn−1 mod pn for each n. Such sequences arise naturally when investigating congruences such as x2 ≡ c mod pn. A more natural representation of a p-adic integer is as
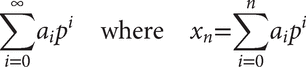
and 0≤ai
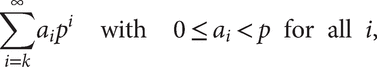
where k is any integer (possibly negative). The p-adic numbers then naturally form a field denoted ℚp.
There is an alternative analytic construction of ℚp. Any non-zero rational number x can be uniquely written as pn(a/b), where neither a nor b is divisible by p. The order |x|p of x is defined to be p–n, with the order of 0 being 0, and a metric can be defined on ℚ by d(x,y) = |x–y|p. The p-adic numbers can then be constructed as the completion of ℚ using this metric.