q-Dimension
| (1) |
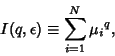 | (2) |
| (3) |
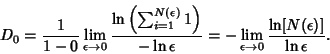 | (4) |
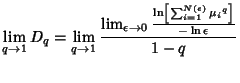 | |||
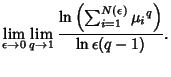 | (5) |
But
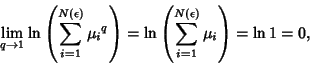 | (6) |
| (7) |
| (8) |
| (9) |
- Abel's Curve Theorem
- Abel's Functional Equation
- Abel's Identity
- Abel's Impossibility Theorem
- Abel's Inequality
- Abel's Irreducibility Theorem
- Abel's Lemma
- Abel's Test
- Abel's Theorem
- Abel's Uniform Convergence Test
- Abel Transform
- Abhyankar's Conjecture
- Ablowitz-Ramani-Segur Conjecture
- Abscissa
- Absolute Convergence
- Absolute Deviation
- Absolute Error
- Absolute Geometry
- Absolutely Continuous
- Absolute Pseudoprime
- Absolute Square
- Absolute Value
- Absorption Law
- Abstraction Operator
- Abundance