| 释义 |
Quadratic FormA quadratic form involving 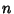 Real variables Real variables 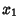 , , 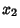 , ..., , ...,  associated with the associated with the  Matrix Matrix 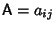 is given by is given by
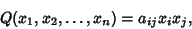 | (1) |
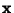 be a Vector made up of be a Vector made up of 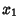 , ..., , ...,  and and  the Transpose, then the Transpose, then
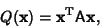 | (2) |
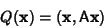 | (3) |
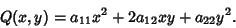 | (4) |
It is always possible to express an arbitrary quadratic form
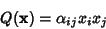 | (5) |
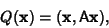 | (6) |
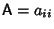 is a Symmetric Matrix given by is a Symmetric Matrix given by
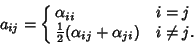 | (7) |
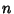 variables may be reduced to the diagonal form variables may be reduced to the diagonal form
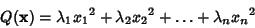 | (8) |
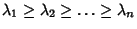 by a suitable orthogonal point-transformation. Also, two realquadratic forms are equivalent under the group of linear transformations Iff they have the same Rank and Signature.See also Disconnected Form, Indefinite Quadratic Form, Inner Product, Integer-Matrix Form,Positive Definite Quadratic Form, Positive Semidefinite Quadratic Form, Rank (Quadratic Form),Signature (Quadratic Form), Sylvester's Inertia Law by a suitable orthogonal point-transformation. Also, two realquadratic forms are equivalent under the group of linear transformations Iff they have the same Rank and Signature.See also Disconnected Form, Indefinite Quadratic Form, Inner Product, Integer-Matrix Form,Positive Definite Quadratic Form, Positive Semidefinite Quadratic Form, Rank (Quadratic Form),Signature (Quadratic Form), Sylvester's Inertia Law
References
 Quadratic Forms Quadratic FormsBuell, D. A. Binary Quadratic Forms: Classical Theory and Modern Computations. New York: Springer-Verlag, 1989. Conway, J. H. and Fung, F. Y. The Sensual (Quadratic) Form. Washington, DC: Math. Assoc. Amer., 1998. Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, pp. 1104-106, 1979. Lam, T. Y. The Algebraic Theory of Quadratic Forms. Reading, MA: W. A. Benjamin, 1973.
|
![]() Real variables
Real variables ![]() ,
, ![]() , ...,
, ..., ![]() associated with the
associated with the ![]() Matrix
Matrix ![]() is given by
is given by![]() Quadratic Forms
Quadratic Forms