| 释义 |
Hanning FunctionAn Apodization Function, also called the Hann Function, frequently used to reduce Aliasing inFourier Transforms. The illustrations above show the Hanning function, its InstrumentFunction, and a blowup of the Instrument Function sidelobes. The Hanning function is given by
 | (1) |
 | (2) |
 . It has Apparatus Function . It has Apparatus Function
The first integral is
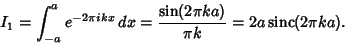 | (4) |
Combining (4) and (5) gives
 | (6) |
To find the extrema, define  and rewrite (6) as and rewrite (6) as
 | (7) |
 | (8) |
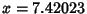 and 10.7061, giving a peak Negative sidelobe of and 10.7061, giving a peak Negative sidelobe of 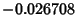 and a peakPositive sidelobe (in units of and a peakPositive sidelobe (in units of  ) of 0.00843441. The peak in units of ) of 0.00843441. The peak in units of  is 1, and the full-width at half maximum isgiven by setting (7) equal to 1/2 and solving for is 1, and the full-width at half maximum isgiven by setting (7) equal to 1/2 and solving for  , yielding , yielding
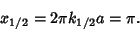 | (9) |
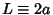 , the Full Width at Half Maximum is , the Full Width at Half Maximum is
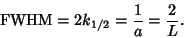 | (10) |
|









![]() and rewrite (6) as
and rewrite (6) as