Schröder Number
The Schröder number ![]() is the number of Lattice Paths in the Cartesian plane that start at(0, 0), end at
is the number of Lattice Paths in the Cartesian plane that start at(0, 0), end at ![]() , contain no points above the line
, contain no points above the line ![]() , and are composed only of steps (0, 1), (1, 0), and (1,1), i.e.,
, and are composed only of steps (0, 1), (1, 0), and (1,1), i.e., ![]() ,
, ![]() , and
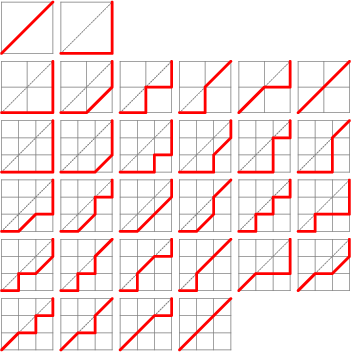
, and ![]() . The diagrams illustrating the paths generating
. The diagrams illustrating the paths generating ![]() ,
, ![]() , and
, and ![]() are illustrated above. The numbers
are illustrated above. The numbers ![]() are given by the Recurrence Relation
are given by the Recurrence Relation

where
References
Sloane, N. J. A. SequenceA006318/M1659in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
- Supergraph
- Supernormal
- Superperfect Number
- Superposition Principle
- Super-Poulet Number
- Superregular Graph
- Superscript
- Superset
- Supplementary Angle
- Support
- Support Function
- Supremum
- Supremum Limit
- Surd
- Surface
- Surface Area
- Surface Integral
- Surface of Revolution
- Surface of Section
- Surface Parameterization
- Surgery
- Surjection
- Surjective
- Surprise Examination Paradox
- Surreal Number