| 释义 |
MomentThe 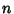 th moment of a distribution about zero th moment of a distribution about zero  is defined by is defined by
 | (1) |
 | (2) |
 , the Mean, is usually simply denoted , the Mean, is usually simply denoted  . If the moment is instead taken about a point . If the moment is instead taken about a point  , ,
 | (3) |
 and are defined by and are defined by
 | (4) |
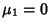 . The moments about zero and about the Mean are related by . The moments about zero and about the Mean are related by
The second moment about the Mean is equal to the Variance
 | (8) |
 is called the Standard Deviation. is called the Standard Deviation.
The related Characteristic Function is defined by
 | (9) |
 | (10) |
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Moments of a Distribution: Mean, Variance, Skewness, and So Forth.'' §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.
|
![]() th moment of a distribution about zero
th moment of a distribution about zero ![]() is defined by
is defined by