Aristotle's Wheel Paradox

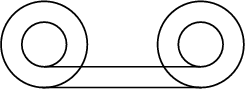
A Aristotle. Consider theabove diagram depicting a wheel consisting of two concentric Circles of different Diameters (a wheel within a wheel). There is a 1:1 correspondence of points on the large Circle with points on thesmall Circle, so the wheel should travel the same distance regardless of whether it is rolled from left to right on thetop straight line or on the bottom one. This seems to imply that the two Circumferences of differentsized Circles are equal, which is impossible.

The fallacy lies in the assumption that a 1:1 correspondence of points means that two curves must have the same length. Infact, the Cardinalities of points in a Line Segment of any length (or even an InfiniteLine, a Plane, a 3-D Space, or an infinite dimensional Euclidean Space) are all the same: (Aleph-1), so the points of any of these can be put in a One-to-One correspondence with those ofany other.

References

Ballew, D. ``The Wheel of Aristotle.'' Math. Teacher 65, 507-509, 1972.

Costabel, P. ``The Wheel of Aristotle and French Consideration of Galileo's Arguments.'' Math. Teacher 61, 527-534, 1968.

Drabkin, I. ``Aristotle's Wheel: Notes on the History of the Paradox.'' Osiris 9, 162-198, 1950.

Gardner, M. Wheels, Life, and other Mathematical Amusements. New York: W. H. Freeman, pp. 2-4, 1983.

Pappas, T. ``The Wheel of Paradox Aristotle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 202, 1989.

vos Savant, M. The World's Most Famous Math Problem. New York: St. Martin's Press, pp. 48-50, 1993.

• Closed Disk
• Closed Form
• Closed Graph Theorem
• Closed Interval
• Closed Set
• Close Packing
• Closure
• Clothoid
• Clove Hitch
• Clump
• Cluster
• Cluster Perimeter
• C-Matrix
• Coanalytic Set
• Coastline Paradox
• Coates-Wiles Theorem
• Coaxal Circles
• Coaxaloid System
• Coaxal System
• Cobordant Manifold
• Cobordism
• Cobordism Group
• Cobordism Ring
• Cochleoid
• Cochleoid Inverse Curve