Singular Point (Differential Equation)
Consider a second-order Ordinary Differential Equation
If
and 
remain Finite at 
, then 
is called an Ordinary Point. If either or diverges as 
, then is called a singular point. Singular points are furtherclassified as follows:- 1. If either 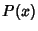or diverges as 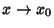but
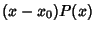and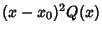 
remain Finiteas 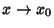, then 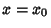is called a Regular Singular Point (or Nonessential Singularity). - 2. If 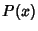diverges more quickly than
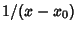, so 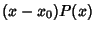approaches Infinity as 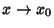,or diverges more quickly than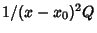 
so that 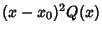goes to Infinity as 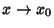, then is called an Irregular Singularity (or Essential Singularity).
References
Arfken, G. ``Singular Points.'' §8.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 451-454, 1985.
- Repunit
- Residual
- Residual vs. Predictor Plot
- Residue Class
- Residue (Complex Analysis)
- Residue (Congruence)
- Residue Index
- Residue Theorem (Complex Analysis)
- Residue Theorem (Group)
- Resolution
- Resolution Class
- Resolution Modulus
- Resolvable
- Resolving Tree
- Resonance Overlap
- Resonance Overlap Method
- R-Estimate
- Restricted Divisor Function
- Restricted Growth Function
- Restricted Growth String
- Resultant
- Retardance
- Reuleaux Polygon
- Reuleaux Triangle
- Reversal