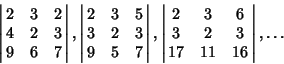| 释义 |
DeterminantDeterminants are mathematical objects which are very useful in the analysis and solution of systems of linear equations. Asshown in Cramer's Rule, a nonhomogeneous system of linear equations has a nontrivial solution Iff thedeterminant of the system's Matrix is Nonzero (so that the Matrix is nonsingular). A 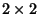 determinant is defined to be determinant is defined to be
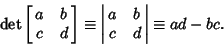 | (1) |
 determinant can be expanded by Minors to obtain determinant can be expanded by Minors to obtain | |  | (2) |
A general determinant for a Matrix A has a value
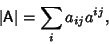 | (3) |
 and where and where  is the Cofactor of is the Cofactor of  defined by defined by
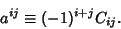 | (4) |
 Matrix formed by eliminating row Matrix formed by eliminating row  and column and column  from A, i.e., by Determinant Expansion by Minors. from A, i.e., by Determinant Expansion by Minors.
Given an  determinant, the additive inverse is determinant, the additive inverse is
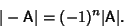 | (5) |
 | (6) |
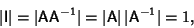 | (7) |
 | (8) |
 | (9) |
 | (10) |
 | (11) |
The determinant of a Matrix Transpose equals the determinant of the original Matrix,
 | (13) |
 | (14) |
Let  be a small number. Then be a small number. Then
 | (15) |
 is the Trace of A. The determinant takes on a particularly simple form for aTriangular Matrix is the Trace of A. The determinant takes on a particularly simple form for aTriangular Matrix
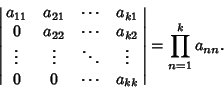 | (16) |
Important properties of the determinant include the following. - 1. Switching two rows or columns changes the sign.
- 2. Scalars can be factored out from rows and columns.
- 3. Multiples of rows and columns can be added together without changing the determinant's value.
- 4. Scalar multiplication of a row by a constant
 multiplies the determinant by multiplies the determinant by  . . - 5. A determinant with a row or column of zeros has value 0.
- 6. Any determinant with two rows or columns equal has value 0.
Property 1 can be established by induction. For a 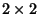 Matrix, the determinant is Matrix, the determinant is
For a  Matrix, the determinant isProperty 2 follows likewise. For Matrix, the determinant isProperty 2 follows likewise. For 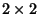 and and  matrices, matrices,
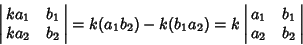 | (19) |
 | (20) |
 | |  | (21) |
If  is an is an  Matrix with Matrix with  Real Numbers, then Real Numbers, then 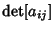 has the interpretation as the oriented has the interpretation as the oriented  -dimensional Content of the Parallelepiped spannedby the column vectors -dimensional Content of the Parallelepiped spannedby the column vectors  , ..., , ...,  in in 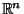 . Here, ``oriented'' means that, up to a change of . Here, ``oriented'' means that, up to a change of  or or Sign, the number is the Sign, the number is the  -dimensional Content, but the Sign depends on the ``orientation'' ofthe column vectors involved. If they agree with the standard orientation, there is a -dimensional Content, but the Sign depends on the ``orientation'' ofthe column vectors involved. If they agree with the standard orientation, there is a  Sign; if not, there is a Sign; if not, there is a Sign. The Parallelepiped spanned by the Sign. The Parallelepiped spanned by the  -D vectors -D vectors 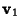 through through  is the collectionof points is the collectionof points
 | (22) |
 is a Real Number in the Closed Interval [0,1]. is a Real Number in the Closed Interval [0,1].
There are an infinite number of  determinants with no 0 or determinants with no 0 or  entries having unity determinant. Oneparametric family is entries having unity determinant. Oneparametric family is
 | (23) |
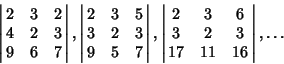 | (24) |
References
Arfken, G. ``Determinants.'' §4.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 168-176, 1985.Guy, R. K. ``Unsolved Problems Come of Age.'' Amer. Math. Monthly 96, 903-909, 1989. Guy, R. K. ``A Determinant of Value One.'' §F28 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 265-266, 1994.
|
![]() determinant is defined to be
determinant is defined to be

![]() determinant, the additive inverse is
determinant, the additive inverse is

![]() be a small number. Then
be a small number. Then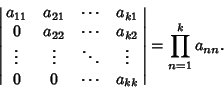
 multiplies the determinant by
multiplies the determinant by  .
.
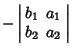


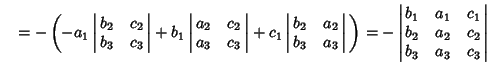
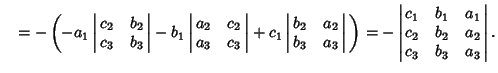



![]() is an
is an ![]() Matrix with
Matrix with ![]() Real Numbers, then
Real Numbers, then ![]() has the interpretation as the oriented
has the interpretation as the oriented ![]() -dimensional Content of the Parallelepiped spannedby the column vectors
-dimensional Content of the Parallelepiped spannedby the column vectors ![]() , ...,
, ..., ![]() in
in ![]() . Here, ``oriented'' means that, up to a change of
. Here, ``oriented'' means that, up to a change of ![]() or
or![]() Sign, the number is the
Sign, the number is the ![]() -dimensional Content, but the Sign depends on the ``orientation'' ofthe column vectors involved. If they agree with the standard orientation, there is a
-dimensional Content, but the Sign depends on the ``orientation'' ofthe column vectors involved. If they agree with the standard orientation, there is a ![]() Sign; if not, there is a
Sign; if not, there is a![]() Sign. The Parallelepiped spanned by the
Sign. The Parallelepiped spanned by the ![]() -D vectors
-D vectors ![]() through
through ![]() is the collectionof points
is the collectionof points![]() determinants with no 0 or
determinants with no 0 or ![]() entries having unity determinant. Oneparametric family is
entries having unity determinant. Oneparametric family is