| 释义 |
Bernoulli NumberThere are two definitions for the Bernoulli numbers. The older one, no longer in widespread use, defines theBernoulli numbers  by the equations by the equations
for  , or , or
for  (Whittaker and Watson 1990, p. 125). Gradshteyn and Ryzhik (1979) denote these numbers (Whittaker and Watson 1990, p. 125). Gradshteyn and Ryzhik (1979) denote these numbers  , whileBernoulli numbers defined by the newer (National Bureau of Standards) definition are denoted , whileBernoulli numbers defined by the newer (National Bureau of Standards) definition are denoted  . The . The  Bernoullinumbers may be calculated from the integral Bernoullinumbers may be calculated from the integral
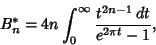 | (4) |
 | (5) |
 , 2, ..., where , 2, ..., where  is the Riemann Zeta Function. is the Riemann Zeta Function.
The first few Bernoulli numbers  are are
Bernoulli numbers defined by the modern definition are denoted  and also called ``Even-index'' Bernoulli numbers. These arethe Bernoulli numbers returned by the Mathematica and also called ``Even-index'' Bernoulli numbers. These arethe Bernoulli numbers returned by the Mathematica (Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones (Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones  since since
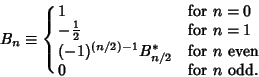 | (6) |
 can be defined by the identity can be defined by the identity
 | (7) |
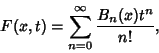 | (8) |
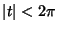 and all and all  (Castellanos 1988). Taking the partial derivative gives (Castellanos 1988). Taking the partial derivative gives
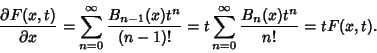 | (9) |
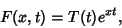 | (10) |
or
 | (12) |
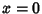 and adding and adding  to both sides then gives to both sides then gives
 | (13) |
 then gives then gives
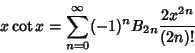 | (14) |
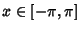 . The Bernoulli numbers may also be calculated from the integral . The Bernoulli numbers may also be calculated from the integral
 | (15) |
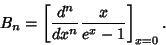 | (16) |
The Bernoulli numbers satisfy the identity
 | (17) |
 is a Binomial Coefficient. An asymptotic Formula is is a Binomial Coefficient. An asymptotic Formula is
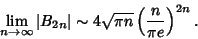 | (18) |
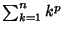 , where , where  , 2, .... Bernoulli numbers also appear inthe series expansions of functions involving , 2, .... Bernoulli numbers also appear inthe series expansions of functions involving 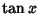 , ,  , ,  , ,  , ,  , ,  , , , , 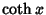 , and , and  . An analytic solution exists for Even orders, . An analytic solution exists for Even orders,
 | (19) |
 , 2, ..., where , 2, ..., where  is the Riemann Zeta Function. Another intimate connection with the Riemann Zeta Function is provided by the identity is the Riemann Zeta Function. Another intimate connection with the Riemann Zeta Function is provided by the identity
 | (20) |
The Denominator of  is given by the von Staudt-Clausen Theorem is given by the von Staudt-Clausen Theorem
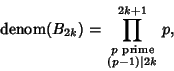 | (21) |
 is Squarefree (Hardy and Wright 1979). Another curiousproperty is that the fraction part of is Squarefree (Hardy and Wright 1979). Another curiousproperty is that the fraction part of  in Decimal has a Decimal Period which divides in Decimal has a Decimal Period which divides 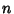 , and there isa single digit before that period (Conway 1996). , and there isa single digit before that period (Conway 1996).
(Sloane's A000367and A002445). In addition,
 | (22) |
 , 2, .... , 2, ....
Bernoulli first used the Bernoulli numbers while computing 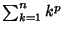 . He used the property of the FigurateNumber Triangle that . He used the property of the FigurateNumber Triangle that
 | (23) |
 which he derived inductively to compute the sums up to which he derived inductively to compute the sums up to  (Boyer 1968, p. 85). For (Boyer 1968, p. 85). For 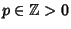 , the sum is given by , the sum is given by
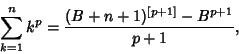 | (24) |
 means the quantity in question is raised to the appropriate Power means the quantity in question is raised to the appropriate Power  , and all terms of theform , and all terms of theform  are replaced with the corresponding Bernoulli numbers are replaced with the corresponding Bernoulli numbers  . Written explicitly in terms of a sum of Powers, . Written explicitly in terms of a sum of Powers,
 | (25) |
 gave a number of curious infinite sum identities involving Bernoulli numbers (Berndt 1994). gave a number of curious infinite sum identities involving Bernoulli numbers (Berndt 1994).
G. J. Fee and S. Plouffe have computed  , which has , which has 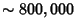 Digits (Plouffe). Plouffeand collaborators have also calculated Digits (Plouffe). Plouffeand collaborators have also calculated  for for 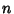 up to 72,000. up to 72,000. See also Argoh's Conjecture, Bernoulli Function, Bernoulli Polynomial, Debye Functions,Euler-Maclaurin Integration Formulas, Euler Number, Figurate Number Triangle, Genocchi Number, Pascal's Triangle,Riemann Zeta Function, von Staudt-Clausen Theorem
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula.'' §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.Arfken, G. ``Bernoulli Numbers, Euler-Maclaurin Formula.'' §5.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338, 1985. Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 71, 1987. Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 81-85, 1994. Boyer, C. B. A History of Mathematics. New York: Wiley, 1968. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 107-110, 1996. Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, 1980. Hardy, G. H. and Wright, W. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 91-93, 1979. Ireland, K. and Rosen, M. ``Bernoulli Numbers.'' Ch. 15 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-248, 1990. Knuth, D. E. and Buckholtz, T. J. ``Computation of Tangent, Euler, and Bernoulli Numbers.'' Math. Comput. 21, 663-688, 1967. Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computationof Constants.'' http://www.lacim.uqam.ca/pi/records.html. Ramanujan, S. ``Some Properties of Bernoulli's Numbers.'' J. Indian Math. Soc. 3, 219-234, 1911. Sloane, N. J. A. SequencesA000367/M4039and A002445/M4189in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Spanier, J. and Oldham, K. B. ``The Bernoulli Numbers,  .'' Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987. .'' Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987. Wagstaff, S. S. Jr. ``Ramanujan's Paper on Bernoulli Numbers.'' J. Indian Math. Soc. 45, 49-65, 1981. Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
|
![]() by the equations
by the equations
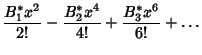
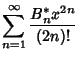
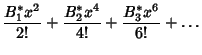

![]() are
are![]() and also called ``Even-index'' Bernoulli numbers. These arethe Bernoulli numbers returned by the Mathematica
and also called ``Even-index'' Bernoulli numbers. These arethe Bernoulli numbers returned by the Mathematica![]() (Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones
(Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones ![]() since
since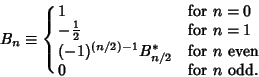

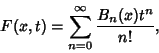
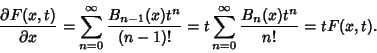
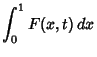
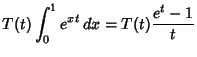
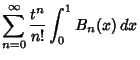



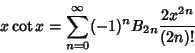

![]() is given by the von Staudt-Clausen Theorem
is given by the von Staudt-Clausen Theorem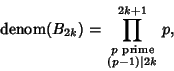
![]() . He used the property of the FigurateNumber Triangle that
. He used the property of the FigurateNumber Triangle that 
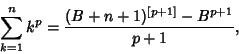

![]() , which has
, which has ![]() Digits (Plouffe). Plouffeand collaborators have also calculated
Digits (Plouffe). Plouffeand collaborators have also calculated ![]() for
for ![]() up to 72,000.
up to 72,000.![]() .'' Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
.'' Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.