| 释义 |
Bernoulli PolynomialThere are two definitions of Bernoulli polynomials in use. The 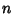 th Bernoulli polynomial is denoted here by th Bernoulli polynomial is denoted here by  ,and the archaic Bernoulli polynomial by ,and the archaic Bernoulli polynomial by  . These definitions correspond to the Bernoulli Numbers evaluated at 0, . These definitions correspond to the Bernoulli Numbers evaluated at 0,
They also satisfy
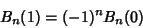 | (3) |
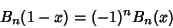 | (4) |
Bernoulli (1713) defined the polynomials in terms of sums of the Powers of consecutive integers,
 | (5) |
 in terms of the generating function in terms of the generating function
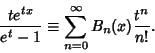 | (6) |
 | (7) |
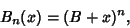 | (8) |
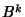 is interpreted here as is interpreted here as 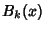 . Hurwitz gave the Fourier Series . Hurwitz gave the Fourier Series
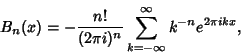 | (9) |
 , and Raabe (1851) found , and Raabe (1851) found
 | (10) |
A sum identity involving the Bernoulli Polynomials is
 | (11) |
 and arbitrary Real Numbers and arbitrary Real Numbers 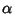 and and  .See also Bernoulli Number, Euler-Maclaurin Integration Formulas, Euler Polynomial .See also Bernoulli Number, Euler-Maclaurin Integration Formulas, Euler Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula.'' §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.Appell, P. E. ``Sur une classe de polynomes.'' Annales d'École Normal Superieur, Ser. 2 9, 119-144, 1882. Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 330, 1985. Bernoulli, J. Ars conjectandi. Basel, Switzerland, p. 97, 1713. Published posthumously. Euler, L. ``Methodus generalis summandi progressiones.'' Comment. Acad. Sci. Petropol. 6, 68-97, 1738. Lehmer, D. H. ``A New Approach to Bernoulli Polynomials.'' Amer. Math. Monthly. 95, 905-911, 1988. Lucas, E. Ch. 14 in Théorie des Nombres. Paris, 1891. Raabe, J. L. ``Zurückführung einiger Summen und bestimmten Integrale auf die Jakob Bernoullische Function.'' J. reine angew. Math. 42, 348-376, 1851. Spanier, J. and Oldham, K. B. ``The Bernoulli Polynomial  .'' Ch. 19 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 167-173, 1987. .'' Ch. 19 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 167-173, 1987.
|

![]() th Bernoulli polynomial is denoted here by
th Bernoulli polynomial is denoted here by ![]() ,and the archaic Bernoulli polynomial by
,and the archaic Bernoulli polynomial by ![]() . These definitions correspond to the Bernoulli Numbers evaluated at 0,
. These definitions correspond to the Bernoulli Numbers evaluated at 0, 
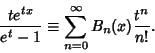
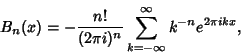


![]() .'' Ch. 19 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 167-173, 1987.
.'' Ch. 19 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 167-173, 1987.