| 释义 |
Bessel Differential Equation
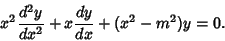 | (1) |
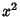 , ,
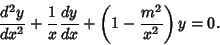 | (2) |
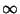 . .
A transformed version of the Bessel differential equation given by Bowman (1958) is
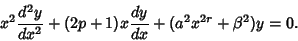 | (3) |
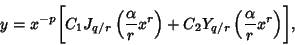 | (4) |
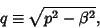 | (5) |
 and and 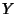 are the Bessel Functions of the First andSecond Kinds, and are the Bessel Functions of the First andSecond Kinds, and 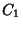 and and  are constants. Another formis given by letting are constants. Another formis given by letting 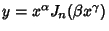 , , 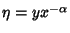 , and , and 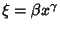 (Bowman 1958, p. 117),then (Bowman 1958, p. 117),then
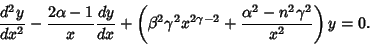 | (6) |
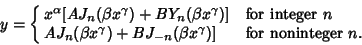 | (7) |
References
Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 550, 1953.
|