Norm
Given a ![]() -D Vector
-D Vector
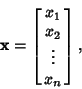
a Vector Norm
- 1.
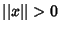 when
when 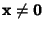 and
and 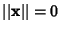 Iff
Iff 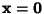 ,
, - 2.
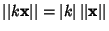 for any Scalar
for any Scalar  ,
, - 3.
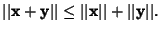
Given a Square Matrix ![]() , a Matrix Norm
, a Matrix Norm ![]() is a Nonnegative number associated with
is a Nonnegative number associated with ![]() having the properties
having the properties
- 1.
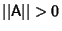 when
when 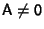 and
and 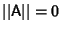 Iff
Iff 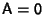 ,
, - 2.
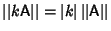 for any Scalar
for any Scalar  ,
, - 3.
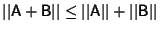 ,
, - 4.
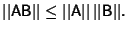
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, pp. 1114-1125, 1979.
- XOR
- Yacht
- Yanghui Triangle
- y-Axis
- Yff Center of Congruence
- Yff Points
- Yff Triangles
- y-Intercept
- Yin-Yang
- Young Diagram
- Young Girl-Old Woman Illusion
- Young Inequality
- Young's Integral
- Young Tableau
- Z
- Z-
- Z+
- Z*
- Zag Number
- Zarankiewicz's Conjecture
- Zariski Topology
- Zaslavskii Map
- Zassenhaus-Berlekamp Algorithm
- z-Axis
- z-Distribution