| 释义 |
Spherical Bessel Differential EquationTake the Helmholtz Differential Equation
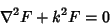 | (1) |
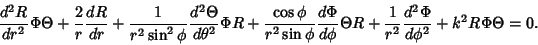 | (2) |
 , ,
 | (3) |
 . Call the separation constant . Call the separation constant  , ,
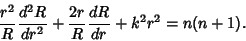 | (4) |
 , ,
 | (5) |
 , then , then
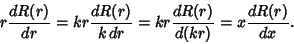 | (6) |
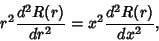 | (7) |
 | (8) |
 , denoting a derivative with respect to , denoting a derivative with respect to 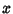 by a prime, by a prime,
so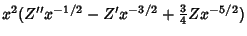 | |  | | | (11) |
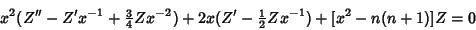 | (12) |
 | (13) |
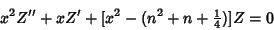 | (14) |
 | (15) |
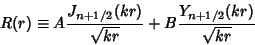 | (16) |
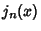 (Spherical Bessel Function of the First Kind) or (Spherical Bessel Function of the First Kind) or  (Spherical Bessel Function of the SecondKind), and the general solution is written (Spherical Bessel Function of the SecondKind), and the general solution is written
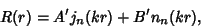 | (17) |
See also Spherical Bessel Function, Spherical Bessel Function of the First Kind, Spherical Bessel Function ofthe Second Kind
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 437, 1972.
|

