Bézier Curve

Given a set of ![]() control points, the corresponding Bézier curve (or Bernstein-Bézier Curve) is given by
control points, the corresponding Bézier curve (or Bernstein-Bézier Curve) is given by
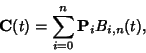
where
A ``rational'' Bézier curve is defined by
where
The Bézier curve always passes through the first and last control points and lies within the Convex Hull of thecontrol points. The curve is tangent to ![]() and
and ![]() at the endpoints. The``variation diminishing property'' of these curves is that no line can have more intersections with a Bézier curve thanwith the curve obtained by joining consecutive points with straight line segments. A desirable property of these curves isthat the curve can be translated and rotated by performing these operations on the control points.
at the endpoints. The``variation diminishing property'' of these curves is that no line can have more intersections with a Bézier curve thanwith the curve obtained by joining consecutive points with straight line segments. A desirable property of these curves isthat the curve can be translated and rotated by performing these operations on the control points.
Undesirable properties of Bézier curves are their numerical instability for large numbers of control points, and thefact that moving a single control point changes the global shape of the curve. The former is sometimes avoided bysmoothly patching together low-order Bézier curves. A generalization of the Bézier curve is the B-Spline.
See also B-Spline, NURBS Curve- Wave Equation
- Wavelet
- Wavelet Matrix
- Wavelet Transform
- Wave Operator
- Wave Surface
- Weak Convergence
- Weak Law of Large Numbers
- Weakly Binary Tree
- Weakly Complete Sequence
- Weakly Independent
- Weakly Triple-Free Set
- Weber Differential Equations
- Weber Functions
- Weber's Discontinuous Integrals
- Weber's Formula
- Weber-Sonine Formula
- Weber's Theorem
- Web Graph
- Wedderburn's Theorem
- Weddle's Rule
- Wedge
- Wedge Product
- Weekday
- Weibull Distribution