Catalan Number
The Catalan numbers are an Integer Sequence ![]() which appears in Tree enumeration problems of the type,``In how many ways can a regular
which appears in Tree enumeration problems of the type,``In how many ways can a regular ![]() -gon be divided into
-gon be divided into ![]() Triangles if different orientations arecounted separately?'' (Euler's Polygon Division Problem). The solution is the Catalan number
Triangles if different orientations arecounted separately?'' (Euler's Polygon Division Problem). The solution is the Catalan number ![]() (Dörrie 1965,Honsberger 1973), as graphically illustrated below (Dickau).
(Dörrie 1965,Honsberger 1973), as graphically illustrated below (Dickau).
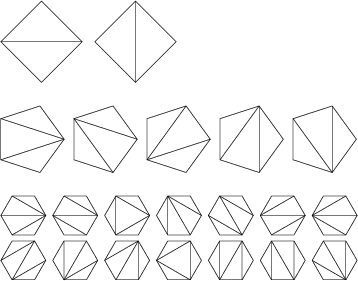
The first few Catalan numbers are 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, ... (Sloane's A000108). The only OddCatalan numbers are those of the form ![]() , and the last Digit is five for
, and the last Digit is five for ![]() to 15. The only PrimeCatalan numbers for
to 15. The only PrimeCatalan numbers for ![]() are
are ![]() and
and ![]() .
.
The Catalan numbers turn up in many other related types of problems. For instance, the Catalan number ![]() gives thenumber of Binary Bracketings of
gives thenumber of Binary Bracketings of ![]() letters (Catalan's Problem). The Catalan numbers also give thesolution to the Ballot Problem, the number of trivalent Planted Planar Trees (Dickau),
letters (Catalan's Problem). The Catalan numbers also give thesolution to the Ballot Problem, the number of trivalent Planted Planar Trees (Dickau),

the number of states possible in an ![]() -Flexagon, the number of different diagonals possible in a FriezePattern with
-Flexagon, the number of different diagonals possible in a FriezePattern with ![]() rows, the number of ways of forming an
rows, the number of ways of forming an ![]() -fold exponential, the number of rooted planar binary treeswith
-fold exponential, the number of rooted planar binary treeswith ![]() internal nodes, the number of rooted plane bushes with
internal nodes, the number of rooted plane bushes with ![]() Edges, the number of extendedBinary Trees with
Edges, the number of extendedBinary Trees with ![]() internal nodes, the number of mountains which can be drawn with
internal nodes, the number of mountains which can be drawn with ![]() upstrokesand
upstrokesand ![]() downstrokes, the number of noncrossing handshakes possible across a round table between
downstrokes, the number of noncrossing handshakes possible across a round table between ![]() pairs of people(Conway and Guy 1996), and the number of Sequences with Nonnegative Partial Sums which can be formed from
pairs of people(Conway and Guy 1996), and the number of Sequences with Nonnegative Partial Sums which can be formed from ![]() 1s and
1s and ![]()
![]() s (Bailey 1996, Brualdi 1997)!
s (Bailey 1996, Brualdi 1997)!
An explicit formula for ![]() is given by
is given by
| (1) |
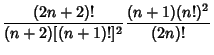 | |||
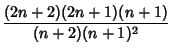 | |||
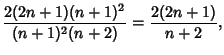 | (2) |
so
| (3) |
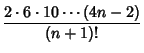 | (4) | ||
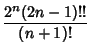 | (5) | ||
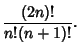 | (6) |
Segner's Recurrence Formula, given by Segner in 1758, gives the solution to Euler's Polygon DivisionProblem
| (7) |
The Generating Function for the Catalan numbers is given by
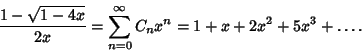 | (8) |
| (9) |
A generalization of the Catalan numbers is defined by
| (10) |
A further generalization is obtained as follows. Let ![]() be an Integer
be an Integer ![]() , let
, let ![]() with
with ![]() , and
, and ![]() . Then define
. Then define ![]() and let
and let ![]() be the number of p-Good Pathfrom (1,
be the number of p-Good Pathfrom (1, ![]() ) to
) to ![]() (Hilton and Pederson 1991). Formulas for
(Hilton and Pederson 1991). Formulas for ![]() include the generalized JonahFormula
include the generalized JonahFormula
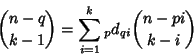 | (11) |
| (12) |
| (13) |
References
Alter, R. ``Some Remarks and Results on Catalan Numbers.'' Proc. 2nd Louisiana Conf. Comb., Graph Th., and Comput., 109-132, 1971. Alter, R. and Kubota, K. K. ``Prime and Prime Power Divisibility of Catalan Numbers.'' J. Combin. Th. 15, 243-256, 1973. Bailey, D. F. ``Counting Arrangements of 1's and Brualdi, R. A. Introductory Combinatorics, 3rd ed. New York: Elsevier, 1997. Campbell, D. ``The Computation of Catalan Numbers.'' Math. Mag. 57, 195-208, 1984. Chorneyko, I. Z. and Mohanty, S. G. ``On the Enumeration of Certain Sets of Planted Trees.'' J. Combin. Th. Ser. B 18, 209-221, 1975. Chu, W. ``A New Combinatorial Interpretation for Generalized Catalan Numbers.'' Disc. Math. 65, 91-94, 1987. Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 96-106, 1996. Dershowitz, N. and Zaks, S. ``Enumeration of Ordered Trees.'' Disc. Math. 31, 9-28, 1980. Dickau, R. M. ``Catalan Numbers.'' http://forum.swarthmore.edu/advanced/robertd/catalan.html. Dörrie, H. ``Euler's Problem of Polygon Division.'' §7 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 21-27, 1965. Eggleton, R. B. and Guy, R. K. ``Catalan Strikes Again! How Likely is a Function to be Convex?'' Math. Mag. 61, 211-219, 1988. Gardner, M. ``Catalan Numbers.'' Ch. 20 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, 1988. Gardner, M. ``Catalan Numbers: An Integer Sequence that Materializes in Unexpected Places.'' Sci. Amer. 234, 120-125, June 1976. Gould, H. W. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, 6th ed. Morgantown, WV: Math Monongliae, 1985. Graham, R. L.; Knuth, D. E.; and Patashnik, O. Exercise 9.8 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994. Guy, R. K. ``Dissecting a Polygon Into Triangles.'' Bull. Malayan Math. Soc. 5, 57-60, 1958. Hilton, P. and Pederson, J. ``Catalan Numbers, Their Generalization, and Their Uses.'' Math. Int. 13, 64-75, 1991. Honsberger, R. Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 130-134, 1973. Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 146-150, 1985. Klarner, D. A. ``Correspondences Between Plane Trees and Binary Sequences.'' J. Comb. Th. 9, 401-411, 1970. Rogers, D. G. ``Pascal Triangles, Catalan Numbers and Renewal Arrays.'' Disc. Math. 22, 301-310, 1978. Sands, A. D. ``On Generalized Catalan Numbers.'' Disc. Math. 21, 218-221, 1978. Singmaster, D. ``An Elementary Evaluation of the Catalan Numbers.'' Amer. Math. Monthly 85, 366-368, 1978. Sloane, N. J. A. A Handbook of Integer Sequences. Boston, MA: Academic Press, pp. 18-20, 1973. Sloane, N. J. A. SequenceA000108/M1459in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and extended entry inSloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 187-188 and 198-199, 1991. Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin, pp. 121-122, 1986.![]() 's.'' Math. Mag. 69, 128-131, 1996.
's.'' Math. Mag. 69, 128-131, 1996.
- Biquadratefree
- Biquadratic Equation
- Biquadratic Number
- Biquadratic Reciprocity Theorem
- Biquaternion
- Birational Transformation
- Birch Conjecture
- Birch-Swinnerton-Dyer Conjecture
- Birkhoff's Ergodic Theorem
- Birotunda
- Birthday Attack
- Birthday Problem
- Bisected Perimeter Point
- Bisection Procedure
- Bisector
- Bishop's Inequality
- Bishops Problem
- Bislit Cube
- Bispherical Coordinates
- Bitangent
- Bit Complexity
- Bivariate Distribution
- Bivector
- Biweight
- Blackman Function