Catenary
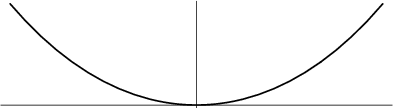
The curve a hanging flexible wire or chain assumes when supported at its ends and acted upon by a uniform gravitationalforce. The word catenary is derived from the Latin word for ``chain.'' In 1669, Jungius disprovedGalileo's 
claim that the curve of a chain hanging under gravity would be a Parabola(MacTutor Archive). The curve is also called the Alysoid and Chainette. The equation was obtainedby Leibniz, Huygens, and Johann Bernoulli in 1691 inresponse to a challenge by Jakob Bernoulli.
Huygens was the first to use the term catenary in a letter to Leibniz in 1690, and David Gregory wrote a treatise on the catenary in 1690 (MacTutor Archive). If you roll a Parabola along a straight line, itsEuler in 1744, the catenary is also the curve which, when rotated,gives the surface of minimum Surface Area (the Catenoid) for the given bounding Circle.
The parametric equations for the catenary are given by
 |  |  | (1) |
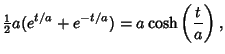 | |  | (2) |
and the Cesàro Equation is
 | (3) |
-gon, the Cartesian equation of the corresponding catenary is
, where 
.
The Arc Length, Curvature, and Tangential Angle are
 | |  | (4) |
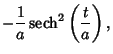 | |  | (5) |
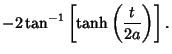 | |  | (6) |
The slope is proportional to the Arc Length as measured from the center of symmetry.See also Calculus of Variations, Catenoid, Lindelof's Theorem, Surface of Revolution
References
Geometry Center. ``The Catenary.'' http://www.geom.umn.edu/zoo/diffgeom/surfspace/catenoid/catenary.html. Gray, A. ``The Evolute of a Tractrix is a Catenary.'' §5.3 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 80-81, 1993. Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 195 and 199-200, 1972. Lockwood, E. H. ``The Tractrix and Catenary.'' Ch. 13 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 118-124, 1967. MacTutor History of Mathematics Archive. ``Catenary.''http://www-groups.dcs.st-and.ac.uk/~history/Curves/Catenary.html. Pappas, T. ``The Catenary & the Parabolic Curves.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 34, 1989. Yates, R. C. ``Catenary.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 12-14, 1952.
- Cyclotomic Equation
- Cyclotomic Factorization
- Cyclotomic Field
- Cyclotomic Integer
- Cyclotomic Invariant
- Cyclotomic Number
- Cyclotomic Polynomial
- Cylinder
- Cylinder Cutting
- Cylinder-Cylinder Intersection
- Cylinder Function
- Cylinder-Sphere Intersection
- Cylindrical Coordinates
- Cylindrical Equal-Area Projection
- Cylindrical Equidistant Projection
- Cylindrical Function
- Cylindrical Harmonics
- Cylindrical Hoof
- Cylindrical Projection
- Cylindrical Segment
- Cylindrical Wedge
- Cylindroid
- Daisy
- d'Alembertian Operator
- d'Alembert Ratio Test