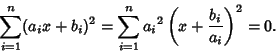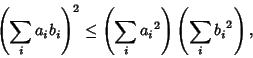| 释义 |
Cauchy InequalityA special case of the Hölder Sum Inequality with 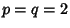 , ,
 | (1) |
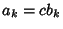 . In 2-D, it becomes . In 2-D, it becomes
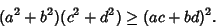 | (2) |
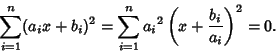 | (3) |
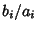 is a constant is a constant  , then , then 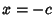 . If it is not a constant, then all terms cannot simultaneously vanish forReal . If it is not a constant, then all terms cannot simultaneously vanish forReal 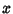 , so the solution is Complex and can be found using theQuadratic Equation , so the solution is Complex and can be found using theQuadratic Equation
 | (4) |
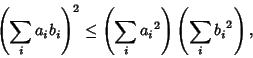 | (5) |
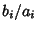 is a constant. The Vector derivation is much simpler, is a constant. The Vector derivation is much simpler,
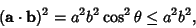 | (6) |
 | (7) |
 .See also Chebyshev Inequality, Hölder Sum Inequality .See also Chebyshev Inequality, Hölder Sum Inequality
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.
|
![]() ,
,