| 释义 |
Helmholtz Differential Equation--Circular Cylindrical CoordinatesIn Cylindrical Coordinates, the Scale Factors are  , , 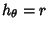 , , 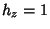 and the separation functions are and the separation functions are 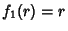 , , 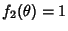 , , 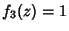 , so the Stäckel Determinant is 1. Attempt Separation of Variables by writing , so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
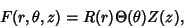 | (1) |
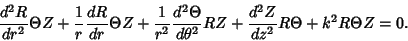 | (2) |
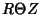 , ,
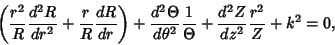 | (3) |
 from the definition of the circularcylindrical coordinate system, the solution to the second part of (3) must have a Negative separation constant from the definition of the circularcylindrical coordinate system, the solution to the second part of (3) must have a Negative separation constant
 | (4) |
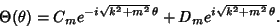 | (5) |
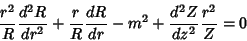 | (6) |
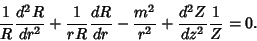 | (7) |
The solution to the second part of (7) must not be sinusoidal at  for a physical solution, so thedifferential equation has a Positive separation constant for a physical solution, so thedifferential equation has a Positive separation constant
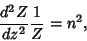 | (8) |
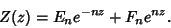 | (9) |
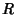 yields yields
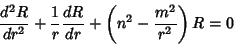 | (10) |
 | (11) |
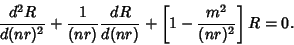 | (12) |
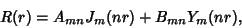 | (13) |
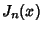 and and 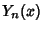 are Bessel Functions of the First andSecond Kinds, respectively. The general solution is therefore are Bessel Functions of the First andSecond Kinds, respectively. The general solution is therefore | |  | (14) |
Actually, the Helmholtz Differential Equation is separable for general 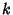 of the form of the form
 | (15) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 656-657, 1953. |
![]() ,
, ![]() ,
, ![]() and the separation functions are
and the separation functions are ![]() ,
, ![]() ,
, ![]() , so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
, so the Stäckel Determinant is 1. Attempt Separation of Variables by writing![]() for a physical solution, so thedifferential equation has a Positive separation constant
for a physical solution, so thedifferential equation has a Positive separation constant![]() of the form
of the form