“Tautochrone Problem”的概念、定义、习题解题方法及翻译-数学辞典

单词

Tautochrone Problem

释义

Tautochrone Problem

Find the curve down which a bead placed anywhere will fall to the bottom in the same amount of time. The solution is aHuygens in Horologium oscillatorium (1673).Huygens also constructed the first pendulum clock with a device to ensure that thependulum was isochronous by forcing the pendulum to swing in an arc of a Cycloid.

The parametric equations of the Cycloid are

			(1)
			(2)

To see that the Cycloid satisfies the tautochrone property, consider the derivatives

			(3)
			(4)

and


			(5)

Now

(6)

(7)


			(8)

so the time required to travel from the top of the Cycloid to the bottom is

(9)

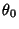However, from an intermediate point

(10)



			(11)

Now let

			(12)
			(13)

(14)

and the amount of time is the same from any point!

See also Brachistochrone Problem, Cycloid

References

Muterspaugh, J.; Driver, T.; and Dick, J. E. ``The Cycloid and Tautochronism.'' http://php.indiana.edu/~jedick/project/intro.html.

Muterspaugh, J.; Driver, T.; and Dick, J. E. ``P221 Tautochrone Problem.'' http://php.indiana.edu/~jedick/project/project.html.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 54-60 and 384-385, 1991.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。