“Logarithmic Binomial Theorem”的概念、定义、习题解题方法及翻译-数学辞典

单词

Logarithmic Binomial Theorem

释义

Logarithmic Binomial Theorem

For all integers and ,

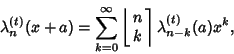
where

is the Harmonic Logarithm and

is a Roman Coefficient. For

, the logarithmic binomial theorem reduces to the classical Binomial Theorem for Positive

, since

for

, and

when

Similarly, taking and gives theNegative Binomial Series. Roman (1992) gives expressions obtained for the case and which are notobtainable from the Binomial Theorem.

See also Harmonic Logarithm, Roman Coefficient

References

Roman, S. ``The Logarithmic Binomial Formula.'' Amer. Math. Monthly 99, 641-648, 1992.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。