“Colorable”的概念、定义、习题解题方法及翻译-数学辞典

单词

Colorable

释义

Colorable

Color each segment of a Knot Diagram using one of three colors. If

: 1. at any crossing, either the colors are all different or all the same, and
: 2. at least two colors are used,

then a Knot is said to be colorable (or more specifically, Three-Colorable). Colorability is invariant underReidemeister Moves, and can be generalized. For instance, for five colors 0, 1, 2, 3, and 4, a Knot isfive-colorable if

: 1. at any crossing, three segments meet. If the overpass is numbered 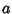and the two underpasses and 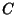, then 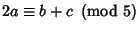, and
: 2. at least two colors are used.

Colorability cannot alway distinguish Handedness. For instance, three-colorability can distinguish the mirrorimages of the Trefoil Knot but not the Figure-of-Eight Knot. Five-colorability, on the other hand,distinguishes the Mirror Images of the Figure-of-Eight Knot but not the Trefoil Knot.

See also Coloring

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。