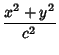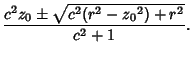| 释义 |
Cone-Sphere IntersectionLet a Cone of opening parameter 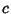 and vertex at and vertex at 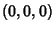 intersect a Sphere ofRadius intersect a Sphere ofRadius  centered at centered at  , with the Cone oriented such that its axis does not pass through thecenter of the Sphere. Then the equations of the curve of intersection are , with the Cone oriented such that its axis does not pass through thecenter of the Sphere. Then the equations of the curve of intersection are
Combining (1) and (2) gives
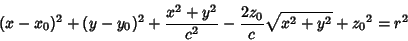 | (3) |
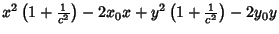 | | 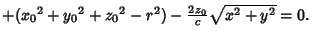 | (4) |
Therefore,  and and  are connected by a complicated Quartic Equation, and are connected by a complicated Quartic Equation, and  , ,  , and , and  by a QuadraticEquation. by a QuadraticEquation.
If the Cone-Sphere intersection is on-axis so that a Cone of opening parameter 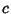 and vertex at and vertex at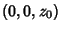 is oriented with its Axis along a radial of the Sphere of radius is oriented with its Axis along a radial of the Sphere of radius  centered at centered at 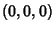 , thenthe equations of the curve of intersection are , thenthe equations of the curve of intersection are
Combining (5) and (6) gives
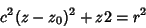 | (7) |
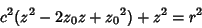 | (8) |
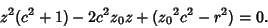 | (9) |
So the curve of intersection is planar. Plugging (10) into (5) shows that the curve is actually a Circle,with Radius given by
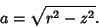 | (11) |
|
![]() and vertex at
and vertex at ![]() intersect a Sphere ofRadius
intersect a Sphere ofRadius ![]() centered at
centered at ![]() , with the Cone oriented such that its axis does not pass through thecenter of the Sphere. Then the equations of the curve of intersection are
, with the Cone oriented such that its axis does not pass through thecenter of the Sphere. Then the equations of the curve of intersection are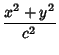
![]() and vertex at
and vertex at![]() is oriented with its Axis along a radial of the Sphere of radius
is oriented with its Axis along a radial of the Sphere of radius ![]() centered at
centered at ![]() , thenthe equations of the curve of intersection are
, thenthe equations of the curve of intersection are