| 释义 |
Confocal Ellipsoidal CoordinatesThe confocal ellipsoidal coordinates (called simply ellipsoidal coordinates by Morse and Feshbach 1953) are given by the equations
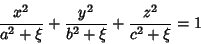 | (1) |
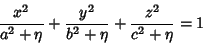 | (2) |
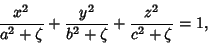 | (3) |
 , , 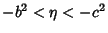 , and , and  . Surfaces of constant . Surfaces of constant 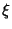 are confocalEllipsoids, surfaces of constant are confocalEllipsoids, surfaces of constant  are one-sheeted Hyperboloids, andsurfaces of constant are one-sheeted Hyperboloids, andsurfaces of constant 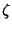 are two-sheeted Hyperboloids. For every are two-sheeted Hyperboloids. For every 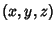 , there is a unique setof ellipsoidal coordinates. However, , there is a unique setof ellipsoidal coordinates. However, 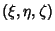 specifies eight points symmetrically located in octants. Solving for specifies eight points symmetrically located in octants. Solving for , ,  , and , and  gives gives
 | (4) |
 | (5) |
 | (6) |
 | |  | | | (7) |
where
 | (8) |
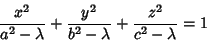 | (9) |
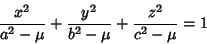 | (10) |
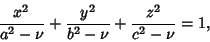 | (11) |
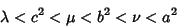 | (12) |
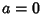 . Equation (9) represents an Ellipsoid, (10) represents aone-sheeted Hyperboloid, and (11) represents a two-sheeted Hyperboloid. In terms ofCartesian Coordinates, . Equation (9) represents an Ellipsoid, (10) represents aone-sheeted Hyperboloid, and (11) represents a two-sheeted Hyperboloid. In terms ofCartesian Coordinates,
 | (13) |
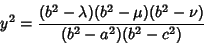 | (14) |
 | (15) |
The Laplacian is
Using the Notation of Byerly (1959, pp. 252-253), this can be reduced to
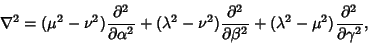 | (20) |
Here,  is an Elliptic Integral of the First Kind. In terms of is an Elliptic Integral of the First Kind. In terms of 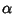 , , 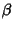 , and , and  , ,
where 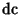 , , 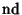 and and 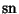 are Jacobi Elliptic Functions. The Helmholtz Differential Equation is separable inconfocal ellipsoidal coordinates.See also Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates are Jacobi Elliptic Functions. The Helmholtz Differential Equation is separable inconfocal ellipsoidal coordinates.See also Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Definition of Elliptical Coordinates.'' §21.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 752, 1972.Arfken, G. ``Confocal Ellipsoidal Coordinates 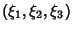 .'' §2.15 in Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970. .'' §2.15 in Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970. Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.
|



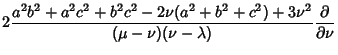


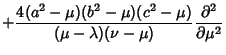
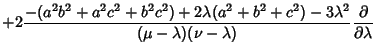
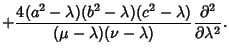
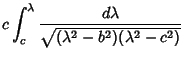
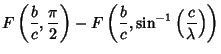
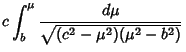
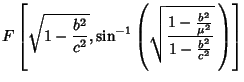
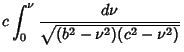
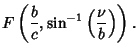
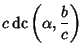

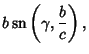
![]() .'' §2.15 in Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.
.'' §2.15 in Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.