Continuous Function
A continuous function is a Function ![]() where the pre-image of every Open Set in
where the pre-image of every Open Set in ![]() is Open in
is Open in ![]() . A function
. A function ![]() in a single variable
in a single variable ![]() is said to be continuous at point
is said to be continuous at point ![]() if
if
- 1.
 is defined, so that
is defined, so that 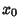 is in the Domain of
is in the Domain of 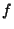 .
. - 2.
 exists for
exists for  in the Domain of
in the Domain of 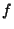 .
. - 3.
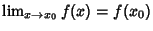 ,
,
- 1.
 is continuous at
is continuous at 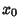 .
. - 2.
 is continuous at
is continuous at 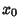 .
. - 3.
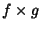 is continuous at
is continuous at 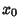 .
. - 4.
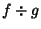 is continuous at
is continuous at 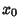 if
if  and is discontinuous at
and is discontinuous at 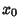 if
if  .
. - 5.
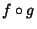 is continuous at
is continuous at 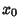 , where
, where 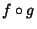 denotes
denotes 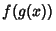 , the Composition of thefunctions
, the Composition of thefunctions 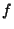 and
and 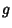 .
.
- For All
- Forcing
- Ford Circle
- Ford's Theorem
- Forest
- Fork
- Form
- Formal Logic
- Form (Geometric)
- Formosa Theorem
- Form (Polynomial)
- Formula
- Fortunate Prime
- Forward Difference
- Fountain
- Four Coins Problem
- Four-Color Theorem
- Fourier-Bessel Series
- Fourier-Bessel Transform
- Fourier Cosine Series
- Fourier Cosine Transform
- Fourier Integral
- Fourier Matrix
- Fourier-Mellin Integral
- Fourier Series