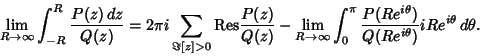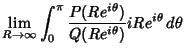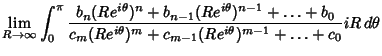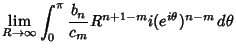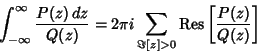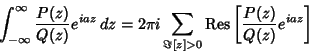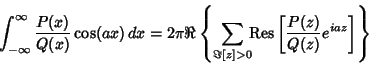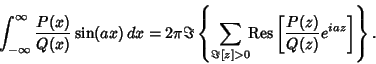| 释义 |
Contour IntegrationLet  and and 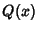 be Polynomials of Degrees be Polynomials of Degrees  and and  withCoefficients withCoefficients 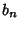 , ..., , ..., 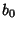 and and 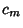 , ..., , ..., 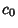 . Take the contour in the upper half-plane, replace . Take the contour in the upper half-plane, replace  by by  ,and write ,and write 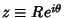 . Then . Then
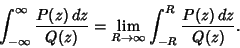 | (1) |
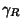 which is straight along the Real axis from which is straight along the Real axis from  to to  and makes a circular arc to connect thetwo ends in the upper half of the Complex Plane. The Residue Theorem thengiveswhere Res denotes the Residues. Solving, and makes a circular arc to connect thetwo ends in the upper half of the Complex Plane. The Residue Theorem thengiveswhere Res denotes the Residues. Solving,
Define
and set
 | (4) |
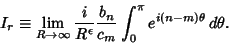 | (5) |
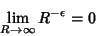 | (6) |
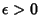 . That means that for . That means that for 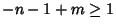 , or , or 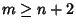 , , , so , so
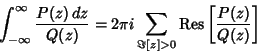 | (7) |
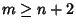 . Apply Jordan's Lemma with . Apply Jordan's Lemma with 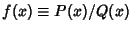 . We must have . We must have
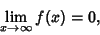 | (8) |
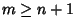 . Then . Then
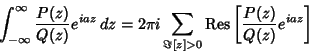 | (9) |
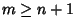 . .
Since this must hold separately for Real and Imaginary Parts, this result can beextended to
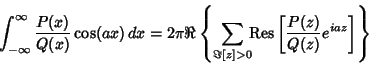 | (10) |
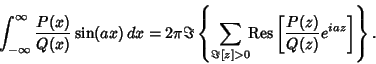 | (11) |
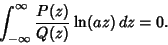 | (12) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 353-356, 1953.
|
![]() and
and ![]() be Polynomials of Degrees
be Polynomials of Degrees ![]() and
and ![]() withCoefficients
withCoefficients ![]() , ...,
, ..., ![]() and
and ![]() , ...,
, ..., ![]() . Take the contour in the upper half-plane, replace
. Take the contour in the upper half-plane, replace ![]() by
by ![]() ,and write
,and write ![]() . Then
. Then