| 释义 |
CosetConsider a countable Subgroup  with Elements with Elements  and an element and an element  not in not in  , then , then
 | (1) |
 | (2) |
 , 2, ... are left and right cosets of the Subgroup , 2, ... are left and right cosets of the Subgroup  with respect to with respect to  . The coset of aSubgroup has the same number of Elements as the Subgroup. The Order of any Subgroup is a divisor of the Order of the Group. The originalGroup can be represented by . The coset of aSubgroup has the same number of Elements as the Subgroup. The Order of any Subgroup is a divisor of the Order of the Group. The originalGroup can be represented by
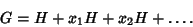 | (3) |
For  a not necessarily Finite Group with a not necessarily Finite Group with  a Subgroup of a Subgroup of  , define an Equivalence Relation , define an Equivalence Relation if if  for some for some 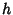 in in  . Then the Equivalence Classes are the left (orright, depending on convention) cosets of . Then the Equivalence Classes are the left (orright, depending on convention) cosets of  in in  , namely the sets , namely the sets
 | (4) |
 is an element of is an element of  .See also Equivalence Class, Group, Subgroup .See also Equivalence Class, Group, Subgroup
|
![]() with Elements
with Elements ![]() and an element
and an element ![]() not in
not in ![]() , then
, then![]() a not necessarily Finite Group with
a not necessarily Finite Group with ![]() a Subgroup of
a Subgroup of ![]() , define an Equivalence Relation
, define an Equivalence Relation![]() if
if ![]() for some
for some ![]() in
in ![]() . Then the Equivalence Classes are the left (orright, depending on convention) cosets of
. Then the Equivalence Classes are the left (orright, depending on convention) cosets of ![]() in
in ![]() , namely the sets
, namely the sets