| 释义 |
Ordinary Differential Equation Second-OrderAn ODE
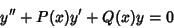 | (1) |
 under the following conditions: (a) If either under the following conditions: (a) If either 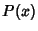 or or  diverges as diverges as  , but , but 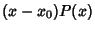 and and  remain finite as remain finite as  , then , then  is called a regular or nonessentialsingular point. (b) If is called a regular or nonessentialsingular point. (b) If 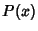 diverges faster than diverges faster than 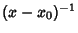 so that so that 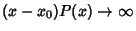 as as  , or , or diverges faster than diverges faster than  so that so that 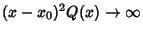 as as  , then , then  is called anirregular or essential singularity. is called anirregular or essential singularity.
Singularities of equation (1) at infinity are investigated by making the substitution  , so , so  , giving , giving
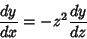 | (2) |
Then (1) becomes
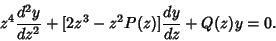 | (4) |
remain finite at 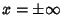 ( (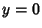 ), then the point is ordinary. Case (b): If either ), then the point is ordinary. Case (b): If either  diverges no morerapidly than diverges no morerapidly than  or or  diverges no more rapidly than diverges no more rapidly than  , then the point is a regular singular point. Case (c): Otherwise, the point is an irregular singular point. , then the point is a regular singular point. Case (c): Otherwise, the point is an irregular singular point.
Morse and Feshbach (1953, pp. 667-674) give the canonical forms and solutions for second-order ODEs classified bytypes of singular points.
For special classes of second-order linear ordinary differential equations, variable Coefficients canbe transformed into constant Coefficients. Given a second-order linear ODE with variableCoefficients
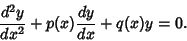 | (7) |
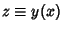 , ,
 | (8) |
 | (9) |
 | (10) |
 | (11) |
 and and 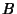 are not functions of are not functions of 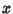 . But we are free to set . But we are free to set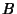 to an arbitrary Positive constant for to an arbitrary Positive constant for  by defining by defining  as as
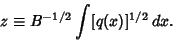 | (12) |
 | (13) |
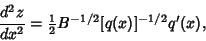 | (14) |
Equation (11) therefore becomes
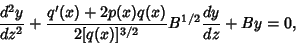 | (16) |
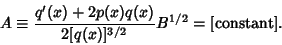 | (17) |
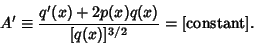 | (18) |
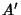 is a constant, the solution is given by solving the second-orderlinear ODE with constant Coefficients is a constant, the solution is given by solving the second-orderlinear ODE with constant Coefficients
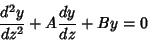 | (19) |
 , where , where  is defined as above. is defined as above.
A linear second-order homogeneous differential equation of the general form
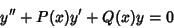 | (20) |
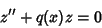 | (21) |
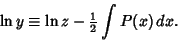 | (22) |
 | (23) |
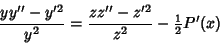 | (24) |
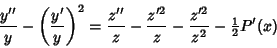 | (25) |
so
Therefore,
 | (28) |
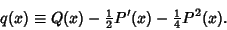 | (29) |
If  , then the differential equation becomes , then the differential equation becomes
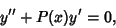 | (30) |
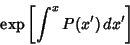 | (31) |
 | (32) |
 | (33) |
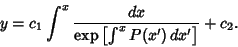 | (34) |
If one solution ( ) to a second-order ODE is known, the other ( ) to a second-order ODE is known, the other (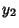 ) may be found using the Reduction ofOrder method. From the Abel's Identity ) may be found using the Reduction ofOrder method. From the Abel's Identity
 | (35) |
 | (36) |
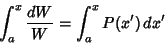 | (37) |
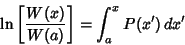 | (38) |
 | (39) |
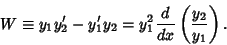 | (40) |
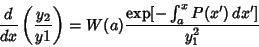 | (41) |
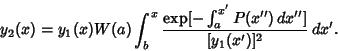 | (42) |
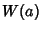 , since it is simply a multiplicative constant, and the constants , since it is simply a multiplicative constant, and the constants  and and 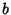 , which will contribute asolution which is not linearly independent of , which will contribute asolution which is not linearly independent of  , ,
 | (43) |
 , this simplifies to , this simplifies to
 | (44) |
For a nonhomogeneous second-order ODE in which the 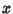 term does not appear in the function term does not appear in the function 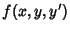 , ,
 | (45) |
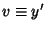 , then , then
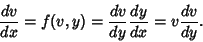 | (46) |
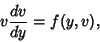 | (47) |
 as a linear first-order ODE. Once the solution is known, as a linear first-order ODE. Once the solution is known,
 | (48) |
 | (49) |
On the other hand, if 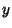 is missing from is missing from 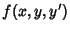 , ,
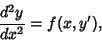 | (50) |
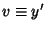 , then , then  , and the equation reduces to , and the equation reduces to
 | (51) |
 as a linear first-order ODE. Once the solution is known, as a linear first-order ODE. Once the solution is known,
 | (52) |
References
Arfken, G. ``A Second Solution.'' §8.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 467-480, 1985.Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, 1986. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 667-674, 1953.
|
![]() , so
, so ![]() , giving
, giving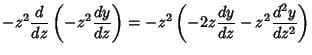
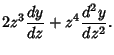



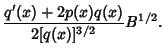
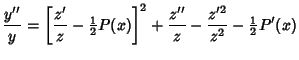

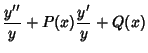
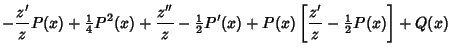
![]() , then the differential equation becomes
, then the differential equation becomes![]() ) to a second-order ODE is known, the other (
) to a second-order ODE is known, the other (![]() ) may be found using the Reduction ofOrder method. From the Abel's Identity
) may be found using the Reduction ofOrder method. From the Abel's Identity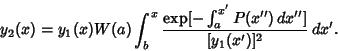

![]() term does not appear in the function
term does not appear in the function ![]() ,
,![]() is missing from
is missing from ![]() ,
,