Hilbert's Problems

A set of (originally) unsolved problems in mathematics proposed by Hilbert. Of the 23 total, ten werepresented at the Second International Congress in Paris in 1900. These problems were designed to serve as examples for thekinds of problems whose solutions would lead to the furthering of disciplines in mathematics.

1a. Is there a transfinite number between that of a Denumerable Set and the numbers of theGödel and Cohen to the effect that the answerdepends on the particular version of Set Theory assumed.

1b. Can the Continuum of numbers be considered a Well-Ordered Set? Thisquestion is related to Zermelo's Axiom of Choice. In 1963, the Axiom of Choice was demonstrated to be independent of all other Axioms in Set Theory, so there appears tobe no universally valid solution to this question either.

2. Can it be proven that the Axioms of logic are consistent? Gödel'sIncompleteness Theorem indicated that the answer is ``no,'' in the sense that any formalsystem interesting enough to formulate its own consistency can prove its own consistency Iff it isinconsistent.

3. Give two Tetrahedra which cannot be decomposed into congruentTetrahedra directly or by adjoining congruent Tetrahedra. Max Dehn showedthis could not be done in 1902. W. F. Kagon obtained the same result independently in 1903.

4. Find Geometries whose Axioms are closest to those ofEuclidean Geometry if the Ordering and Incidence Axioms are retained, theCongruence Axioms weakened, and the equivalent of the Parallel Postulate omitted. This problem was solved by G. Hamel.

5. Can the assumption of differentiability for functions defining a continuoustransformation Group be avoided? (This is a generalization of the Cauchy Functional Equation.) Solved byJohn von Neumann in 1930 for bicompact groups. Also solved for the Abelian case, andfor the solvable case in 1952 with complementary results by Montgomery and Zipin (subsequently combined by Yamabe in1953). Andrew Glean showed in 1952 that the answer is also ``yes'' for all locally bicompact groups.

6. Can physics be axiomized?

7. Let 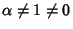be Algebraic and Irrational. Is then Transcendental? Provedtrue in 1934 by Aleksander Gelfond (Gelfond's Theorem; Courant and Robins 1996).

8. Prove the Riemann Hypothesis. The Conjecture has still beenneither proved nor disproved.

9. Construct generalizations of the Reciprocity Theorem of Number Theory.

10. Does there exist a universal algorithm for solving DiophantineEquations? The impossibility ofobtaining a general solution was proven by Julia Robinson and Martin Davis in 1970, following proof of the resultthat the equation (where 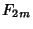is a Fibonacci Number) is Diophantine by Yuri Matijasevich(Matijasevic 1970, Davis 1973, Davis and Hersh 1973, Matijasevic 1993).

11. Extend the results obtained for quadratic fields to arbitrary Integeralgebraic fields.

12. Extend a theorem of Kronecker to arbitrary algebraic fields by explicitlyconstructing Hilbert class fields using special values. This calls for the construction ofHolomorphic Functions in several variables which have properties analogous to the exponential function and ellipticmodular functions (Holzapfel 1995).

13. Show the impossibility of solving the general seventh degree equation byfunctions of two variables.

14. Show the finiteness of systems of relatively integral functions.

15. Justify Schubert's Enumerative Geometry (Bell 1945).

16. Develop a topology of Real algebraic curves and surfaces. The Shimura-Taniyama Conjecture postulates just this connection. See Ilyashenko and Yakovenko(1995) and Gudkov and Utkin (1978).

17. Find a representation of definite form by Squares.

18. Build spaces with congruent Polyhedra.

19. Analyze the analytic character of solutions to variational problems.

20. Solve general Boundary Value Problems.

21. Solve differential equations given a Monodromy Group. More technically,prove that there always exists a Fuchsian System with given singularities and a given Monodromy Group. Several special cases had been solved, but a Negative solution was found in 1989 by B. Bolibruch (Anasov and Bolibruch1994).

22. Uniformization.

23. Extend the methods of Calculus of Variations.

References

Hilbert's Problems

Anasov, D. V. and Bolibruch, A. A. The Riemann-Hilbert Problem. Braunschweig, Germany: Vieweg, 1994.

Bell, E. T. The Development of Mathematics, 2nd ed. New York: McGraw-Hill, p. 340, 1945.

Borowski, E. J. and Borwein, J. M. (Eds.). ``Hilbert Problems.'' Appendix 3 in The Harper Collins Dictionary of Mathematics. New York: Harper-Collins, p. 659, 1991.

Boyer, C. and Merzbach, U. ``The Hilbert Problems.'' History of Mathematics, 2nd ed. New York: Wiley, pp. 610-614, 1991.

Browder, Felix E. (Ed.). Mathematical Developments Arising from Hilbert Problems. Providence, RI: Amer. Math. Soc., 1976.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 107, 1996.

Davis, M. ``Hilbert's Tenth Problem is Unsolvable.'' Amer. Math. Monthly 80, 233-269, 1973.

Davis, M. and Hersh, R. ``Hilbert's 10th Problem.'' Sci. Amer., pp. 84-91, Nov. 1973.

Gudkov, D. and Utkin, G. A. Nine Papers on Hilbert's 16th Problem. Providence, RI: Amer. Math. Soc., 1978.

Holzapfel, R.-P. The Ball and Some Hilbert Problems. Boston, MA: Birkhäuser, 1995.

Ilyashenko, Yu. and Yakovenko, S. (Eds.). Concerning the Hilbert 16th Problem. Providence, RI: Amer. Math. Soc., 1995.

Matijasevic, Yu. V. ``Solution to of the Tenth Problem of Hilbert.'' Mat. Lapok 21, 83-87, 1970.

Matijasevich, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993.

• Bisection Procedure
• Bisector
• Bishop's Inequality
• Bishops Problem
• Bislit Cube
• Bispherical Coordinates
• Bitangent
• Bit Complexity
• Bivariate Distribution
• Bivector
• Biweight
• Blackman Function
• Black-Scholes Theory
• Black Spleenwort Fern
• Blancmange Function
• Blaschke Conjecture
• Blaschke's Theorem
• Blecksmith-Brillhart-Gerst Theorem
• Blichfeldt's Lemma
• Blichfeldt's Theorem
• BLM/Ho Polynomial
• Bloch Constant
• Bloch-Landau Constant
• Block
• Block Design