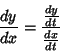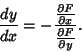| 释义 |
DerivativeThe derivative of a Function represents an infinitesimal change in the function with respect to whatever parameters itmay have. The ``simple'' derivative of a function 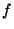 with respect to with respect to 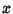 is denoted either is denoted either  or or 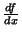 (andoften written in-line as (andoften written in-line as 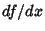 ). When derivatives are taken with respect to time, they are often denoted usingNewton's ). When derivatives are taken with respect to time, they are often denoted usingNewton's  Fluxion notation, Fluxion notation, 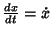 . The derivative of a function . The derivative of a function  withrespect to the variable withrespect to the variable 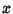 is defined as is defined as
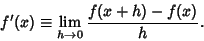 | (1) |
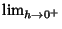 and and 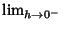 must exist and be equal, so theFunction must be continuous. However, continuity is a Necessary but not Sufficient condition fordifferentiability. Since some Discontinuous functions can be integrated, in a sense there are ``more'' functionswhich can be integrated than differentiated. In a letter to Stieltjes, Hermite must exist and be equal, so theFunction must be continuous. However, continuity is a Necessary but not Sufficient condition fordifferentiability. Since some Discontinuous functions can be integrated, in a sense there are ``more'' functionswhich can be integrated than differentiated. In a letter to Stieltjes, Hermite  wrote, ``I recoil with dismay andhorror at this lamentable plague of functions which do not have derivatives.'' wrote, ``I recoil with dismay andhorror at this lamentable plague of functions which do not have derivatives.''
A 3-D generalization of the derivative to an arbitrary direction is known as the Directional Derivative. In general,derivatives are mathematical objects which exist between smooth functions on manifolds. In this formalism, derivatives areusually assembled into ``Tangent Maps.''
Simple derivatives of some simple functions follow. 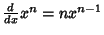 | (2) | 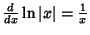 | (3) | 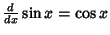 | (4) |  | (5) | 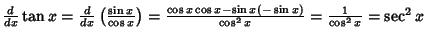 | (6) | 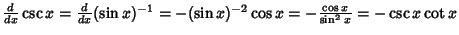 | (7) | 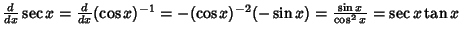 | (8) | 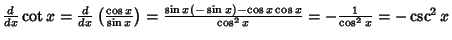 | (9) | 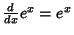 | (10) | 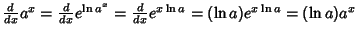 | (11) | 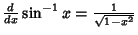 | (12) | 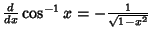 | (13) | 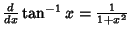 | (14) | 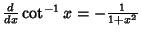 | (15) | 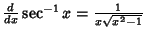 | (16) | 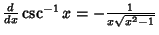 | (17) | 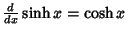 | (18) | 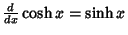 | (19) | 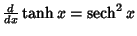 | (20) | 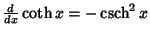 | (21) | 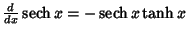 | (22) | 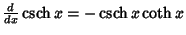 | (23) | 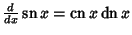 | (24) | 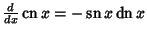 | (25) | 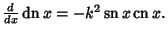 | (26) |
Derivatives of sums are equal to the sum of derivatives so that
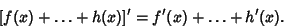 | (27) |
 is a constant, is a constant,
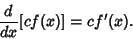 | (28) |
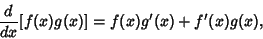 | (29) |
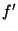 denotes the Derivative of denotes the Derivative of 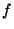 with respect to with respect to 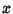 . This derivative rule can be applied iteratively toyield derivate rules for products of three or more functions, for example, . This derivative rule can be applied iteratively toyield derivate rules for products of three or more functions, for example,
Other rules involving derivatives include the Chain Rule, Power Rule, Product Rule, and Quotient Rule. Miscellaneous other derivative identities include
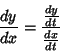 | (31) |
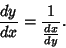 | (32) |
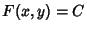 , where , where 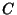 is a constant, then is a constant, then
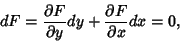 | (33) |
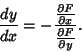 | (34) |
A vector derivative of a vector function
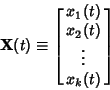 | (35) |
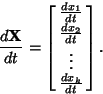 | (36) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.Anton, H. Calculus with Analytic Geometry, 5th ed. New York: Wiley, 1987. Beyer, W. H. ``Derivatives.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 229-232, 1987.
|
![]() with respect to
with respect to ![]() is denoted either
is denoted either ![]() or
or ![]() (andoften written in-line as
(andoften written in-line as ![]() ). When derivatives are taken with respect to time, they are often denoted usingNewton's
). When derivatives are taken with respect to time, they are often denoted usingNewton's ![]() Fluxion notation,
Fluxion notation, ![]() . The derivative of a function
. The derivative of a function ![]() withrespect to the variable
withrespect to the variable ![]() is defined as
is defined as