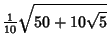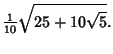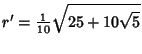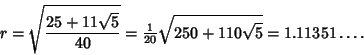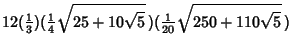| 释义 |
DodecahedronThe regular dodecahedron is the Platonic Solid ( ) composed of 20 Vertices, 30 Edges, and 12 Pentagonal Faces. It is given by the symbol ) composed of 20 Vertices, 30 Edges, and 12 Pentagonal Faces. It is given by the symbol 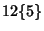 , theSchläfli Symbol , theSchläfli Symbol  . It is also Uniform Polyhedron . It is also Uniform Polyhedron 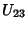 and has WythoffSymbol and has WythoffSymbol 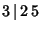 . The dodecahedron has the Icosahedral Group . The dodecahedron has the Icosahedral Group 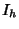 of symmetries. of symmetries.
A Plane Perpendicular to a  axis of a dodecahedron cuts the solid in a regular HexagonalCross-Section (Holden 1991, p. 27). A Plane Perpendicular to a axis of a dodecahedron cuts the solid in a regular HexagonalCross-Section (Holden 1991, p. 27). A Plane Perpendicular to a 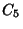 axis of a dodecahedron cuts thesolid in a regular Decagonal Cross-Section (Holden 1991, p. 24). axis of a dodecahedron cuts thesolid in a regular Decagonal Cross-Section (Holden 1991, p. 24).
The Dual Polyhedron of the dodecahedron is the Icosahedron.
When the dodecahedron with edge length  is oriented with two opposite faces parallel to the is oriented with two opposite faces parallel to the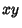 -Plane, the vertices of the top and bottom faces lie at -Plane, the vertices of the top and bottom faces lie at 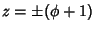 and the other Vertices lie at and the other Vertices lie at  , where , where  is the Golden Ratio. The explicit coordinates are is the Golden Ratio. The explicit coordinates are
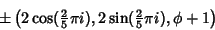 | (1) |
 | (2) |
 , 1, ..., 4, where , 1, ..., 4, where  is the Golden Ratio. Explicitly, these coordinates are is the Golden Ratio. Explicitly, these coordinates are
 |  | 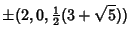 | (3) |  |  | 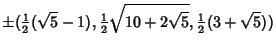 | (4) | 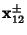 |  |  | (5) |  |  |  | | | | | | (6) |  |  |  | (7) |  |  |  | (8) |  |  |  | (9) |  |  | 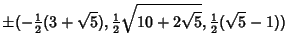 | (10) |  |  |  | | | | | | (11) |  |  |  | (12) |
where  are the top vertices, are the top vertices,  are the vertices above the mid-plane, are the vertices above the mid-plane,  are thevertices below the mid-plane, and are thevertices below the mid-plane, and  are the bottom vertices. The Vertices of adodecahedron can be given in a simple form for a dodecahedron of side length are the bottom vertices. The Vertices of adodecahedron can be given in a simple form for a dodecahedron of side length  by (0, by (0, 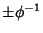 , ,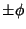 ), ( ), (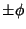 , 0, , 0, 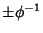 ), ( ), (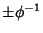 , , 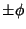 , 0), and ( , 0), and (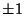 , , 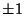 , , 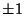 ). ).
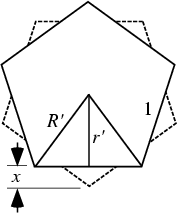
For a dodecahedron of unit edge length 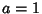 , the Circumradius , the Circumradius  and Inradius and Inradius 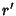 of aPentagonal Face are of aPentagonal Face are
The Sagitta  is then given by is then given by
 | (15) |
Using the Pythagorean Theorem on the figure then gives
Equation (3) can be written
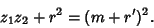 | (19) |
The Inradius of the dodecahedron is then given by
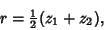 | (23) |
and
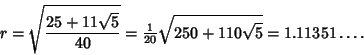 | (25) |
and the Circumradius is
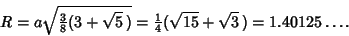 | (27) |
so
 | (29) |
The Area of a single Face is the Area of a Pentagon,
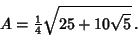 | (30) |
Apollonius  showed that the Volume showed that the Volume  and Surface Area and Surface Area  of the dodecahedron and itsDual the Icosahedron are related by of the dodecahedron and itsDual the Icosahedron are related by
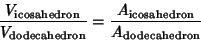 | (32) |
The Hexagonal Scalenohedron is an irregular dodecahedron. See also Augmented Dodecahedron, Augmented Truncated Dodecahedron, Dodecagon,Dodecahedron-Icosahedron Compound, Elongated Dodecahedron,Great Dodecahedron, Great Stellated Dodecahedron, Hyperbolic Dodecahedron, Icosahedron,Metabiaugmented Dodecahedron, Metabiaugmented Truncated Dodecahedron, Parabiaugmented Dodecahedron,Parabiaugmented Truncated Dodecahedron, Pyritohedron, Rhombic Dodecahedron, Small StellatedDodecahedron, Triaugmented Dodecahedron, Triaugmented Truncated Dodecahedron, Trigonal Dodecahedron,Trigonometry Values Pi/5, Truncated Dodecahedron
References
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., 1989.Davie, T. ``The Dodecahedron.'' http://www.dcs.st-and.ac.uk/~ad/mathrecs/polyhedra/dodecahedron.html. Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991.
|

![]() ) composed of 20 Vertices, 30 Edges, and 12 Pentagonal Faces. It is given by the symbol
) composed of 20 Vertices, 30 Edges, and 12 Pentagonal Faces. It is given by the symbol ![]() , theSchläfli Symbol
, theSchläfli Symbol ![]() . It is also Uniform Polyhedron
. It is also Uniform Polyhedron ![]() and has WythoffSymbol
and has WythoffSymbol ![]() . The dodecahedron has the Icosahedral Group
. The dodecahedron has the Icosahedral Group ![]() of symmetries.
of symmetries.![]() axis of a dodecahedron cuts the solid in a regular HexagonalCross-Section (Holden 1991, p. 27). A Plane Perpendicular to a
axis of a dodecahedron cuts the solid in a regular HexagonalCross-Section (Holden 1991, p. 27). A Plane Perpendicular to a ![]() axis of a dodecahedron cuts thesolid in a regular Decagonal Cross-Section (Holden 1991, p. 24).
axis of a dodecahedron cuts thesolid in a regular Decagonal Cross-Section (Holden 1991, p. 24).![]() is oriented with two opposite faces parallel to the
is oriented with two opposite faces parallel to the![]() -Plane, the vertices of the top and bottom faces lie at
-Plane, the vertices of the top and bottom faces lie at ![]() and the other Vertices lie at
and the other Vertices lie at ![]() , where
, where ![]() is the Golden Ratio. The explicit coordinates are
is the Golden Ratio. The explicit coordinates are 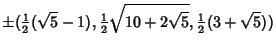




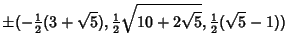


![]() , the Circumradius
, the Circumradius ![]() and Inradius
and Inradius ![]() of aPentagonal Face are
of aPentagonal Face are