Descartes Circle Theorem
A special case of Apollonius' Problem requiring the determination of a Circle touching three mutually tangentCircles (also called the Kissing Circles Problem). There are two solutions: a small circlesurrounded by the three original Circles, and a large circle surrounding the original three. FrederickSoddy gave the Formula for finding the Radius of the so-called inner and outer Soddy Circles given theRadii of the other three. The relationship is
where
are the Curvatures of the Circles. Here, the Negative solutioncorresponds to the outer Soddy Circle and the Positive solution to the inner SoddyCircle. This formula was known to Descartes 
and Viète (Boyer and Merzbach 1991, p. 159), butSoddy extended it to Spheres. In 
-D space, 
mutually touching -Spheres canalways be found, and the relationship of their Curvatures is
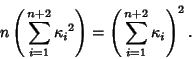
See also Apollonius' Problem, Four Coins Problem, Soddy Circles, Sphere Packing
References
Boyer, C. B. and Merzbach, U. C. A History of Mathematics, 2nd ed. New York: Wiley, 1991. Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 13-16, 1969. Wilker, J. B. ``Four Proofs of a Generalization of the Descartes Circle Theorem.'' Amer. Math. Monthly 76, 278-282, 1969.
- Subspace
- Substitution Group
- Substitution Map
- Subtend
- Subtraction
- Succeeds
- Successes
- Sufficient
- Suitable Number
- Sum
- Summand
- Summatory Function
- Sum-Product Number
- Sum Rule
- Sup
- Characteristic (Partial Differential Equation)
- Characteristic Polynomial
- Characteristic (Real Number)
- Character (Multiplicative)
- Character (Number Theory)
- Character Table
- Charlier's Check
- Chasles-Cayley-Brill Formula
- Chasles's Contact Theorem
- Chasles's Polars Theorem