Valuation
A generalization of the p-adic Number first proposed by Kürschák in 1913. A valuation 
on a Field 
is a Function from to the Real Numbers 
such that thefollowing properties hold for all 
:
- 1.
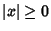, - 2.
Iff 
, - 3.
, - 4.
Implies 
for some constant 
(independent of 
).
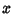If (4) is satisfied for 
, then satisfies the Triangle Inequality,
- 4a.
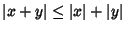for all .
then satisfies the stronger Triangle Inequality- 4b.
.
The simplest valuation is the Absolute Value for Real Numbers. A valuation satisfying (4b) is callednon-Archimedean Valuation; otherwise, it is called Archimedean.
If 
is a valuation on and 
, then we can define a new valuation 
by
 | (1) |
in Axiom 4. If two valuations arerelated in this way, they are said to be equivalent, and this gives an equivalence relation on the collection of allvaluations on . Any valuation is equivalent to one which satisfies the triangle inequality (4a). In view of this, weneed only to study valuations satisfying (4a), and we often view axioms (4) and (4a) as interchangeable (although this isnot strictly true). If two valuations are equivalent, then they are both non-Archimedeanor both Archimedean. 
, , and 
with the usual Euclidean normsare Archimedean valuated fields. For any Prime 
, the p-adic Number 
withthe -adic valuation 
is a non-Archimedean valuated field.
If is any Field, we can define the trivial valuation on by 
for all 
and 
,which is a non-Archimedean valuation. If is a Finite Field, then the only possible valuation over is thetrivial one. It can be shown that any valuation on is equivalent to one of the following: the trivial valuation,Euclidean absolute norm , or -adic valuation .
The equivalence of any nontrivial valuation of to either the usual Absolute Value or to a p-adic Number absolute value was proved by Ostrowski(1935). Equivalent valuations give rise to the same topology. Conversely, if two valuations have the same topology, thenthey are equivalent. A stronger result is the following: Let , , ..., 
be valuationsover which are pairwise inequivalent and let 
, 
, ..., 
be elements of . Then there exists aninfinite sequence (
, 
, ...) of elements of such that
 | (2) |
 | (3) |
with the 3-adic and 5-adic valuations 
and 
, and consider thesequence of numbers given by  | (4) |
as 
with respect to , but 
as with respect to, illustrating that a sequence of numbers can tend to two different limits under two different valuations.A discrete valuation is a valuation for which the Valuation Group is a discrete subset of the RealNumbers . Equivalently, a valuation (on a Field ) is discrete if there exists a RealNumber 
such that
 | (5) |
-adic valuation on is discrete, but the ordinary absolute valuation is not.If is a valuation on , then it induces a metric
 | (6) |
, which in turn induces a Topology on . If satisfies (4b) then the metric is anUltrametric. We say that 
is a complete valuated field if the Metric Space is complete.See also Absolute Value, Local Field, Metric Space, p-adic Number, Strassman's Theorem,Ultrametric, Valuation Group
References
Cassels, J. W. S. Local Fields. Cambridge, England: Cambridge University Press, 1986. Ostrowski, A. ``Untersuchungen zur aritmetischen Theorie der Körper.'' Math. Zeit. 39, 269-404, 1935.
- Cauchy Inequality
- Cauchy Integral Formula
- Cauchy Integral Test
- Cauchy Integral Theorem
- Cauchy-Kovalevskaya Theorem
- Cauchy-Lagrange Identity
- Cauchy-Maclaurin Theorem
- Cauchy Mean Theorem
- Cauchy Principal Value
- Cauchy Problem
- Cauchy Ratio Test
- Cauchy Remainder Form
- Cauchy-Riemann Equations
- Cauchy Root Test
- Cauchy-Schwarz Integral Inequality
- Cauchy-Schwarz Sum Inequality
- Cauchy's Cosine Integral Formula
- Cauchy Sequence
- Cauchy's Formula
- Cauchy's Rigidity Theorem
- Cauchy Test
- Caustic
- Cavalieri's Principle
- Cayley Algebra
- Cayley-Bacharach Theorem