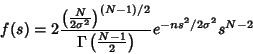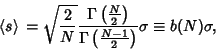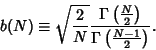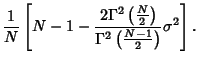| 释义 |
VarianceFor  samples of a variate having a distribution with known Mean samples of a variate having a distribution with known Mean  , the ``populationvariance'' (usually called ``variance'' for short, although the word ``population'' should be added when needed todistinguish it from the Sample Variance) is defined by , the ``populationvariance'' (usually called ``variance'' for short, although the word ``population'' should be added when needed todistinguish it from the Sample Variance) is defined by
where
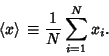 | (2) |
 is an Unbiased Estimator for the Mean is an Unbiased Estimator for the Mean
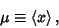 | (3) |
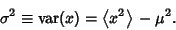 | (4) |
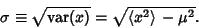 | (5) |
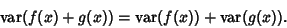 | (6) |
If the population Mean is not known, using the sample mean 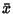 instead of the population mean instead of the population mean  tocompute tocompute
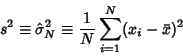 | (9) |
 | (10) |
The Mean and Variance of the sample standard deviation for a distribution with population mean  andVariance are andVariance are
The quantity 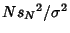 has a Chi-Squared Distribution. has a Chi-Squared Distribution.
For multiple variables, the variance is given using the definition of Covariance,
A linear sum has a similar form:These equations can be expressed using the Covariance Matrix.
To estimate the population Variance from a sample of  elements with a priori unknown Mean (i.e.,the Mean is estimated from the sample itself), we need an Unbiased Estimator for elements with a priori unknown Mean (i.e.,the Mean is estimated from the sample itself), we need an Unbiased Estimator for 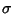 . This is given by the k-Statistic . This is given by the k-Statistic  , where , where
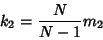 | (15) |
 is the Sample Variance is the Sample Variance
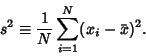 | (16) |
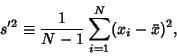 | (17) |
When computing numerically, the Mean must be computed before  can be determined. This requires storing the set ofsample values. It is possible to calculate can be determined. This requires storing the set ofsample values. It is possible to calculate 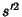 using a recursion relationship involving only the last sample asfollows. Here, use using a recursion relationship involving only the last sample asfollows. Here, use  to denote to denote  calculated from the first calculated from the first  samples (not the samples (not the  th Moment) th Moment)
 | (18) |
 denotes the value for the sample variance denotes the value for the sample variance 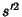 calculated from the first calculated from the first  samples. The first fewvalues calculated for the Mean are samples. The first fewvalues calculated for the Mean are
Therefore, for 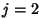 , 3 it is true that , 3 it is true that
 | (22) |
and
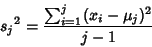 | (26) |
 , so , so
Working on the first term,
Use (24) to write
 | (29) |
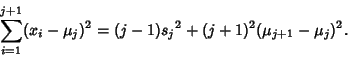 | (30) |
 | (31) |
 | (33) |
so
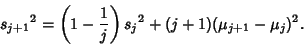 | (36) |
To find the variance of  itself, remember that itself, remember that
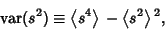 | (37) |
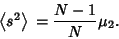 | (38) |
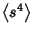 . .
Working on the first term of (39),
The second term of (39) is known from k-Statistic,
 | (41) |
Combining (39)-(42) gives
so plugging in (38) and (43) gives
Student calculated the Skewness and Kurtosis of the distribution of  as as
and conjectured that the true distribution is Pearson Type III Distribution
 | (47) |
This was proven by R. A. Fisher.
The distribution of  itself is given by itself is given by
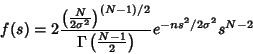 | (50) |
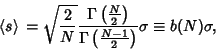 | (51) |
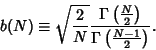 | (52) |
 | (53) |
An Unbiased Estimator of 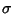 is is 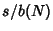 . Romanovsky showed that . Romanovsky showed that
 | (55) |
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Moments of a Distribution: Mean, Variance, Skewness, and So Forth.'' §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.
|
![]() samples of a variate having a distribution with known Mean
samples of a variate having a distribution with known Mean ![]() , the ``populationvariance'' (usually called ``variance'' for short, although the word ``population'' should be added when needed todistinguish it from the Sample Variance) is defined by
, the ``populationvariance'' (usually called ``variance'' for short, although the word ``population'' should be added when needed todistinguish it from the Sample Variance) is defined by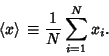
![]() instead of the population mean
instead of the population mean ![]() tocompute
tocompute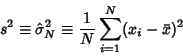

![]() andVariance are
andVariance are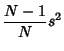
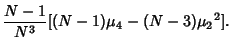
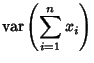
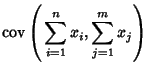




![]() elements with a priori unknown Mean (i.e.,the Mean is estimated from the sample itself), we need an Unbiased Estimator for
elements with a priori unknown Mean (i.e.,the Mean is estimated from the sample itself), we need an Unbiased Estimator for ![]() . This is given by the k-Statistic
. This is given by the k-Statistic ![]() , where
, where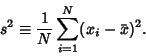
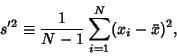
![]() can be determined. This requires storing the set ofsample values. It is possible to calculate
can be determined. This requires storing the set ofsample values. It is possible to calculate ![]() using a recursion relationship involving only the last sample asfollows. Here, use
using a recursion relationship involving only the last sample asfollows. Here, use ![]() to denote
to denote ![]() calculated from the first
calculated from the first ![]() samples (not the
samples (not the ![]() th Moment)
th Moment)

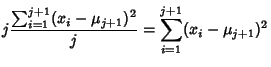
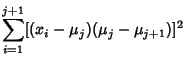


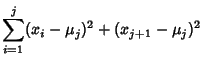
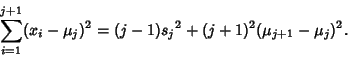


![]() itself, remember that
itself, remember that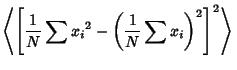

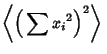
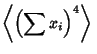

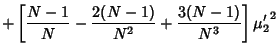
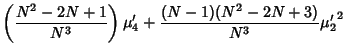





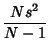
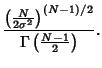
![]() itself is given by
itself is given by