| 释义 |
Digamma FunctionTwo notations are used for the digamma function. The 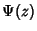 digamma function is defined by digamma function is defined by
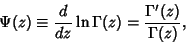 | (1) |
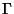 is the Gamma Function, and is the function returned by the function PolyGamma[z] inMathematica is the Gamma Function, and is the function returned by the function PolyGamma[z] inMathematica (Wolfram Research, Champaign, IL). The (Wolfram Research, Champaign, IL). The  digamma function is defined by digamma function is defined by
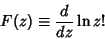 | (2) |
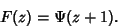 | (3) |
where  is the Euler-Mascheroni Constant and is the Euler-Mascheroni Constant and  are Bernoulli Numbers. are Bernoulli Numbers.
The  th Derivative of th Derivative of 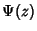 is called the Polygamma Function and is denoted is called the Polygamma Function and is denoted  . Since thedigamma function is the zeroth derivative of . Since thedigamma function is the zeroth derivative of 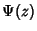 (i.e., the function itself), it is also denoted (i.e., the function itself), it is also denoted 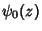 . .
The digamma function satisfies
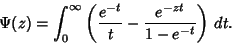 | (9) |
 , ,
 | (10) |
 is the Euler-Mascheroni Constant and is the Euler-Mascheroni Constant and 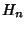 is aHarmonic Number. Other identities include is aHarmonic Number. Other identities include
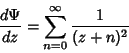 | (11) |
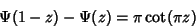 | (12) |
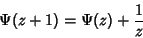 | (13) |
 | (14) |
Special values are
At integral values,
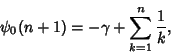 | (17) |
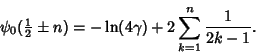 | (18) |
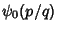 is given by the explicit equation is given by the explicit equation
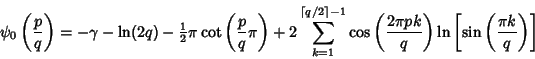 | (19) |
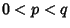 (Knuth 1973). These give the special values (Knuth 1973). These give the special values
where  is the Euler-Mascheroni Constant. Sums and differences of is the Euler-Mascheroni Constant. Sums and differences of 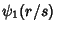 for small integral for small integral 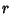 and and 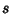 can be expressed in terms of Catalan's Constant and can be expressed in terms of Catalan's Constant and 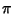 . .
See also Gamma Function, Harmonic Number, Hurwitz Zeta Function, Polygamma Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Psi (Digamma) Function.'' §6.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258-259, 1972.Arfken, G. ``Digamma and Polygamma Functions.'' §10.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 549-555, 1985. Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, p. 94, 1973. Spanier, J. and Oldham, K. B. ``The Digamma Function 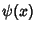 .'' Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987. .'' Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
|
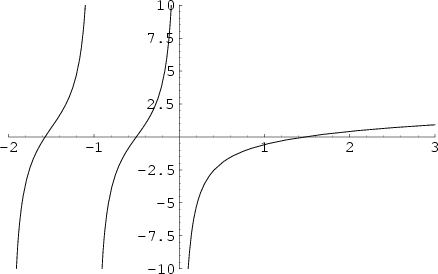
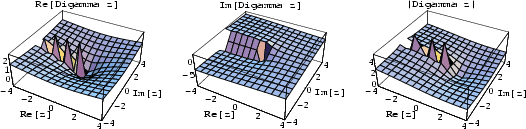
![]() digamma function is defined by
digamma function is defined by


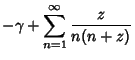
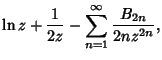
![]() th Derivative of
th Derivative of ![]() is called the Polygamma Function and is denoted
is called the Polygamma Function and is denoted ![]() . Since thedigamma function is the zeroth derivative of
. Since thedigamma function is the zeroth derivative of ![]() (i.e., the function itself), it is also denoted
(i.e., the function itself), it is also denoted ![]() .
.
![]() .'' Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
.'' Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.