| 释义 |
Beltrami IdentityAn identity in Calculus of Variations discovered in 1868 by Beltrami. The Euler-Lagrange DifferentialEquation is
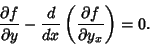 | (1) |

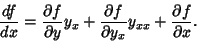 | (2) |
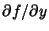 term gives term gives
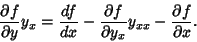 | (3) |
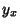 gives gives
 | (4) |
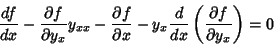 | (5) |
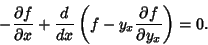 | (6) |
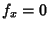 , since in that case , since in that case
 | (7) |
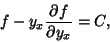 | (8) |
 is a constant of integration. is a constant of integration.
The Beltrami identity greatly simplifies the solution for the minimal Area Surface of Revolution about a givenaxis between two specified points. It also allows straightforward solution of the Brachistochrone Problem. See also Brachistochrone Problem, Calculus of Variations, Euler-Lagrange Differential Equation,Surface of Revolution
|