| 释义 |
Diophantine Equation--6th PowersThe 2-1 equation
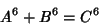 | (1) |
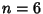 , and so has no solution. Ekl (1996) has searched and found no solutions to the 2-2
 | (2) |
 .
No solutions are known to the 3-1 or 3-2 equations. However, parametric solutions are known for the 3-3 equation
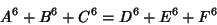 | (3) |
 |  |  | (4) | 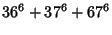 | |  | (5) |  | |  | (6) |  | |  | (7) |  | |  | (8) |  | | 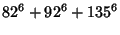 | (9) |  | |  | (10) |  | |  | (11) |  | |  | (12) |  | | 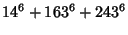 | (13) |
(Rao 1934, Lander et al. 1967).
No solutions are known to the 4-1 or 4-2 equations. The smallest primitive 4-3 solutions are
(Lander et al. 1967). Moessner (1947) gave three parametric solutions to the 4-4 equation. The smallest 4-4 solution is
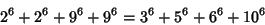 | (19) |
 | (20) |
No  -1 solutions are known for  (Lander et al. 1967). No solution to the 5-1 equation is known (Guy 1994, p. 140) or the 5-2 equation.
No solutions are known to the 6-1 or 6-2 equations.
The smallest 7-1 solution is
 | (21) |
 | (22) |
The smallest primitive 8-1 solutions are
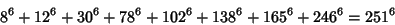 | (23) |
 | (24) |
 | (25) |
 | (26) |
 | (27) |
 | (28) |
 | (29) |
 | (30) |
 | (31) |
 | (32) |
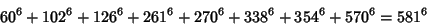 | (33) |
 | (34) |
 | (35) |
 | (36) |
 | (37) |
The smallest 9-1 solution is
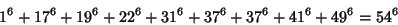 | (38) |
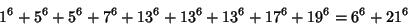 | (39) |
The smallest 10-1 solution is
 | (40) |
 | (41) |
The smallest 11-1 solution is
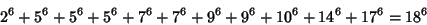 | (42) |
There is also at least one 16-1 identity,  | |  | (43) |
(Martin 1893). Moessner (1959) gave solutions for 16-1, 18-1, 20-1, and 23-1.
References
Ekl, R. L. ``Equal Sums of Four Seventh Powers.'' Math. Comput. 65, 1755-1756, 1996.Guy, R. K. ``Sums of Like Powers. Euler's Conjecture.'' §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994. Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. ``A Survey of Equal Sums of Like Powers.'' Math. Comput. 21, 446-459, 1967. Martin, A. ``On Powers of Numbers Whose Sum is the Same Power of Some Number.'' Quart. J. Math. 26, 225-227, 1893. Moessner, A. ``On Equal Sums of Like Powers.'' Math. Student 15, 83-88, 1947. Moessner, A. ``Einige zahlentheoretische Untersuchungen und diophantische Probleme.'' Glasnik Mat.-Fiz. Astron. Drustvo Mat. Fiz. Hrvatske Ser. 2 14, 177-182, 1959. Rao, S. K. ``On Sums of Sixth Powers.'' J. London Math. Soc. 9, 172-173, 1934.
|
