| 释义 |
Diophantine Equation nth PowersThe 2-1 equation
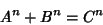 | (1) |
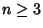 . Lander et al. (1967) give a table showing the smallest . Lander et al. (1967) give a table showing the smallest  for which a solution to for which a solution to
with 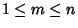 is known. is known.| |  | 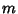 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 1 | 2 | 3 | 3 | 4 | 7 | 8 | 11 | 15 | 23 | | 2 | 2 | 2 | 2 | 4 | 7 | 8 | 9 | 12 | 19 | | 3 | | | | 3 | 3 | 7 | 8 | 11 | 24 | | 4 | | | | | | 4 | 7 | 10 | 23 | | 5 | | | | | | 5 | 5 | 11 | 16 | | 6 | | | | | | | | 6 | 27 | | 7 | | | | | | | | | 7 |
Take the results from the Ramanujan 6-10-8 Identity that for  , with , with 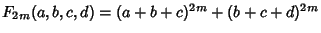 | | 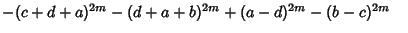 | (2) |
and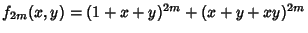 | | 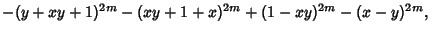 | (3) |
then
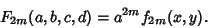 | (4) |
now gives
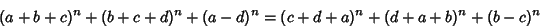 | (7) |
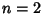 or 4.See also Ramanujan 6-10-8 Identity or 4.See also Ramanujan 6-10-8 Identity
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, p. 101, 1994.Berndt, B. C. and Bhargava, S. ``Ramanujan--For Lowbrows.'' Amer. Math. Monthly 100, 644-656, 1993. Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, pp. 653-657, 1966. Gloden, A. Mehrgradige Gleichungen. Groningen, Netherlands: P. Noordhoff, 1944. Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994. Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. ``A Survey of Equal Sums of Like Powers.'' Math. Comput. 21, 446-459, 1967. Reznick, B. ``Sums of Even Powers of Real Linear Forms.'' Mem. Amer. Math. Soc. No. 463, 96. Providence, RI: Amer. Math. Soc., 1992.
|
![]() , with
, with