| 释义 |
Distribution FunctionThe distribution function 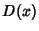 , sometimes also called the Probability Distribution Function, describes theprobability that a trial , sometimes also called the Probability Distribution Function, describes theprobability that a trial  takes on a value less than or equal to a number takes on a value less than or equal to a number  . The distribution function is thereforerelated to a continuous Probability Density Function . The distribution function is thereforerelated to a continuous Probability Density Function  by by
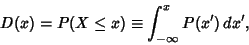 | (1) |
 (when it exists) is simply the derivative of the distribution function (when it exists) is simply the derivative of the distribution function
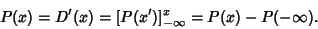 | (2) |
 by by
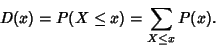 | (3) |
A Joint Distribution Function can be defined if outcomes are dependent on two parameters:
Similarly, a multiple distribution function can be defined if outcomes depend on  parameters: parameters:
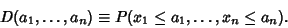 | (7) |
Given a continuous  , assume you wish to generate numbers distributed as , assume you wish to generate numbers distributed as  using a random number generator.If the random number generator yields a uniformly distributed value using a random number generator.If the random number generator yields a uniformly distributed value 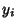 in [0,1] for each trial in [0,1] for each trial 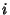 , then compute , then compute
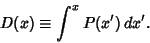 | (8) |
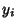 with a variable distributed as with a variable distributed as  is then is then
 | (9) |
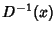 is the inverse function of is the inverse function of 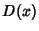 . For example, if . For example, if  were a Gaussian Distribution so that were a Gaussian Distribution so that
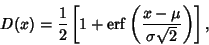 | (10) |
 | (11) |
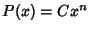 for for 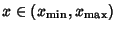 , then normalization gives , then normalization gives
 | (12) |
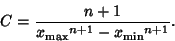 | (13) |
 be a uniformly distributed variate on be a uniformly distributed variate on 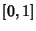 . Then . Then
and the variate given by
is distributed as  . .
A distribution with constant Variance of  for all values of for all values of  is known as a Homoscedastic distribution.The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method. is known as a Homoscedastic distribution.The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method. See also Bernoulli Distribution, Beta Distribution, Binomial Distribution, Bivariate Distribution,Cauchy Distribution, Chi Distribution, Chi-Squared Distribution, Cornish-Fisher AsymptoticExpansion, Correlation Coefficient, Distribution, Double Exponential Distribution, Equally LikelyOutcomes Distribution, Exponential Distribution, Extreme Value Distribution, F-Distribution,Fermi-Dirac Distribution, Fisher's z-Distribution, Fisher-Tippett Distribution, GammaDistribution, Gaussian Distribution, Geometric Distribution, Half-Normal Distribution,Hypergeometric Distribution, Joint Distribution Function, Laplace Distribution, LatticeDistribution, Lévy Distribution, Logarithmic Distribution, Log-SeriesDistribution, Logistic Distribution, Lorentzian Distribution, Maxwell Distribution, NegativeBinomial Distribution, Normal Distribution, Pareto Distribution, Pascal Distribution, Pearson TypeIII Distribution, Poisson Distribution, Pólya Distribution, Ratio Distribution,Rayleigh Distribution, Rice Distribution, Snedecor's F-Distribution, Student's t-Distribution,Student's z-Distribution, Uniform Distribution, Weibull Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Probability Functions.'' Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 925-964, 1972.Iyanaga, S. and Kawada, Y. (Eds.). ``Distribution of Typical Random Variables.'' Appendix A, Table 22 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1483-1486, 1980.
|
![]() , sometimes also called the Probability Distribution Function, describes theprobability that a trial
, sometimes also called the Probability Distribution Function, describes theprobability that a trial ![]() takes on a value less than or equal to a number
takes on a value less than or equal to a number ![]() . The distribution function is thereforerelated to a continuous Probability Density Function
. The distribution function is thereforerelated to a continuous Probability Density Function ![]() by
by![]() , assume you wish to generate numbers distributed as
, assume you wish to generate numbers distributed as ![]() using a random number generator.If the random number generator yields a uniformly distributed value
using a random number generator.If the random number generator yields a uniformly distributed value ![]() in [0,1] for each trial
in [0,1] for each trial ![]() , then compute
, then compute 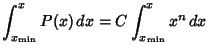
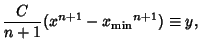

![]() for all values of
for all values of ![]() is known as a Homoscedastic distribution.The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method.
is known as a Homoscedastic distribution.The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method.