| 释义 |
Yff PointsLet points 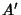 , ,  , and , and 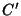 be marked off some fixed distance be marked off some fixed distance 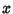 along each of the sides along each of the sides 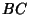 , ,  , and , and 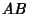 .Then the lines .Then the lines 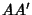 , ,  , and , and 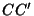 concur in a point concur in a point 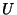 known as the first Yff point if known as the first Yff point if
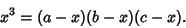 | (1) |
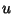 , which can by obtained by solving the Cubic Equation , which can by obtained by solving the Cubic Equation
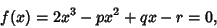 | (2) |
The Isotomic Conjugate Point 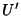 is called the second Yff point. The Triangle Center Functions of the first and second points are given by is called the second Yff point. The Triangle Center Functions of the first and second points are given by
 | (6) |
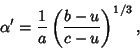 | (7) |
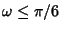 for the Brocard Angle for the Brocard Angle 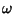 , , 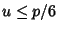 holds for the Yff points, with equality in the case of an Equilateral Triangle. Analogous to holds for the Yff points, with equality in the case of an Equilateral Triangle. Analogous to
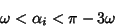 | (8) |
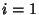 , 2, 3, the Yff points satisfy , 2, 3, the Yff points satisfy
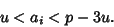 | (9) |
Yff (1963) gives a number of other interesting properties. The line 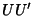 is Perpendicular to the line containingthe Incenter is Perpendicular to the line containingthe Incenter 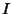 and Circumcenter and Circumcenter  , and its length is given by , and its length is given by
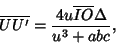 | (10) |
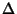 is the Area of the Triangle. See also Brocard Points, Yff Triangles is the Area of the Triangle. See also Brocard Points, Yff Triangles
References
Yff, P. ``An Analog of the Brocard Points.'' Amer. Math. Monthly 70, 495-501, 1963.
|

![]() ,
, ![]() , and
, and ![]() be marked off some fixed distance
be marked off some fixed distance ![]() along each of the sides
along each of the sides ![]() ,
, ![]() , and
, and ![]() .Then the lines
.Then the lines ![]() ,
, ![]() , and
, and ![]() concur in a point
concur in a point ![]() known as the first Yff point if
known as the first Yff point if![]() is Perpendicular to the line containingthe Incenter
is Perpendicular to the line containingthe Incenter ![]() and Circumcenter
and Circumcenter ![]() , and its length is given by
, and its length is given by