Euler-Maclaurin Integration Formulas
The first Euler-Maclaurin integration formula is
 | |
 | |
 | (1) |
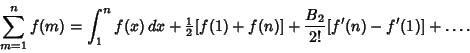are Bernoulli Numbers. Sums may be converted to Integrals by inverting the Formula to obtain | (2) |
is tabulated at 
values 
, 
, ..., 
, | |
 | (3) |
The Euler-Maclaurin formula is implemented in Mathematica
(Wolfram Research, Champaign, IL) as the functionNSum with option Method->Integrate.
The second Euler-Maclaurin integration formula is used when is tabulated at values 
, 
, ...,
:
 | |
 |
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 16 and 806, 1972.
Arfken, G. ``Bernoulli Numbers, Euler-Maclaurin Formula.'' §5.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338, 1985.
Borwein, J. M.; Borwein, P. B.; and Dilcher, K. ``Pi, Euler Numbers, and Asymptotic Expansions.'' Amer. Math. Monthly 96, 681-687, 1989.
Vardi, I. ``The Euler-Maclaurin Formula.'' §8.3 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 159-163, 1991.
- Zermelo Set Theory
- Zernike Polynomial
- Zero
- Zero Divisor
- Zero (Root)
- Zero-Sum Game
- Zeta Fuchsian
- Zeta Function
- Zeuthen's Rule
- Zeuthen's Theorem
- Zig Number
- Zigzag Permutation
- Zig-Zag Triangle
- Zillion
- Zipf's Law
- Z-Number
- Zollner's Illusion
- Zonal Harmonic
- Zone
- Zonohedron
- Zonotype
- Zorn's Lemma
- z-Score
- Zsigmondy Theorem
- Z-Transform